10.5 Graphing Systems of Inequalities
The solution to a system of inequalities is their shared solution set or the regions on the graph that make all inequalities true.
To graph a system of inequalities:
1) Open the Graph window by going to the Menu in the top left.
2) Enter inequalities in the input field and tap the enter key after each one
3) On the graph, find the region representing the shared solution set.
To graph a system of inequalities:
1) Open the Graph window by going to the Menu in the top left.
2) Enter inequalities in the input field and tap the enter key after each one
3) On the graph, find the region representing the shared solution set.
Examples
Solve each system of inequalities below:
Solve each system of inequalities below:
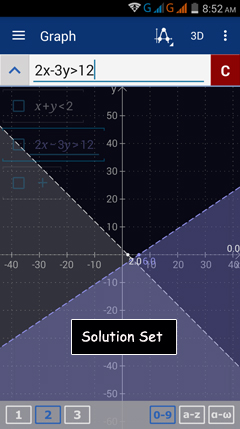
1) 2x – 3y > 12
x + y ≤ 2
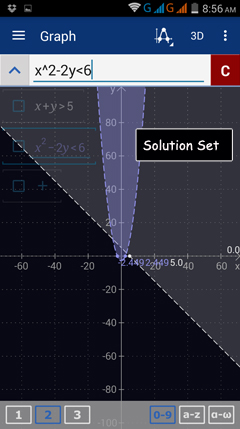
2) x + y ≥ 5
x2 – 2y < 6
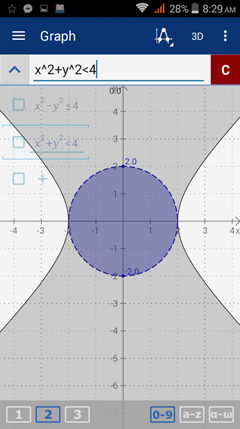
3) x2 – y2 ≤ 4
x2 + y2 < 4
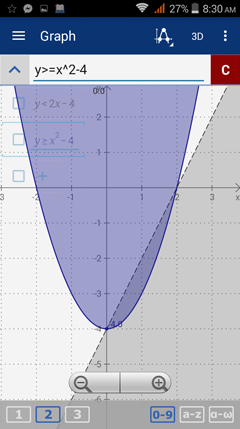
4) y < 2x – 4
y ≥ x2 – 4
x + y ≤ 2
2) x + y ≥ 5
x2 – 2y < 6
3) x2 – y2 ≤ 4
x2 + y2 < 4
4) y < 2x – 4
y ≥ x2 – 4
Calculator solutions
Type the greater than sign ( > ) by tapping the closed parentheses " ) " three times.
Type the less than sign ( < ) by tapping the open parentheses " ( " three times.
Use the variable y by tapping the x variable key twice.
1) Enter the expressions:
2x - 3y > 12 and
x + y < 2 as "x + y <= 2."
Type the greater than sign ( > ) by tapping the closed parentheses " ) " three times.
Type the less than sign ( < ) by tapping the open parentheses " ( " three times.
Use the variable y by tapping the x variable key twice.
1) Enter the expressions:
2x - 3y > 12 and
x + y < 2 as "x + y <= 2."
2) Enter the expressions:
x + y > 5 as "x + y >= 5" and
x^2 - 2y < 6.
x + y > 5 as "x + y >= 5" and
x^2 - 2y < 6.
3) Enter the expressions:
x^2 - y^2 < 4 as "x^2 - y^2 <= 4" and
x^2 + y^2 < 4.
x^2 - y^2 < 4 as "x^2 - y^2 <= 4" and
x^2 + y^2 < 4.
4) Enter the expressions:
y < 2x - 4 and
y > x^2 - 4 as "y >= x^2 - 4."
y < 2x - 4 and
y > x^2 - 4 as "y >= x^2 - 4."