19.5.3. Median of an Ungrouped Data Set
The median refers to the middle data point of an ordered data set at the 50% percentile. If a data set has an odd number of observations, then the median is the middle value. If it has an even number of observations, the median is the average of the two middle values.
The median refers to the middle data point of an ordered data set at the 50% percentile. If a data set has an odd number of observations, then the median is the middle value. If it has an even number of observations, the median is the average of the two middle values.
To find the median:
1) Arrange the data values from least to greatest.
2) If necessary, use the locator's formula c = (n + 1)/2 where n is the total number of observations.
3) Look for the value at (n + 1)/2. Use the result in step 2.
If c contains a fractional half, it means the median is the average of two values. For example, if the location is 3.5, the median is the average of the 3rd and 4th data points.
Illustration
Find the median of each data set.
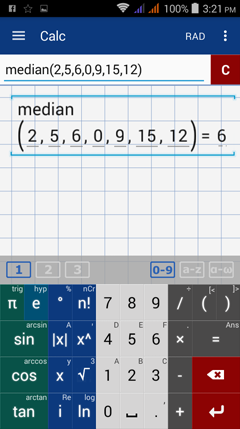
1) 2, 5, 6, 0, 9, 15, 12
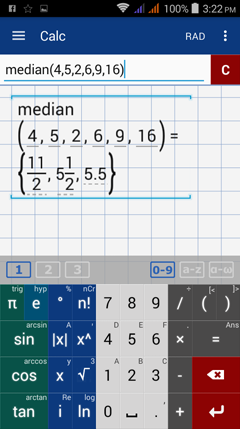
2) 4, 5, 2, 6, 9, 16
Solutions
1) Arrange the data values from least to greatest.
0, 2, 5, 6, 9, 12, 15
Find the middle data point. Since there are seven (odd) observations, the median is the (7+1)/2 = 4th data point. The 4th point is 6 so the median is 6.
2) Arrange the data values from least to greatest.
2, 4, 5, 6, 9, 16
Find the middle data point. Since there are six (even) observations, the median is at (6+1)/2 = 3.5, or the average of the 3rd and 4th data points, (5+6)/2 = 5.5.
Calculator solutions
To find the median, hold the factorial key (n!) and select median. You can also type "median" using the a-z keyboard. Enter the data set in parentheses or in brackets as a matrix.
1) Arrange the data values from least to greatest.
2) If necessary, use the locator's formula c = (n + 1)/2 where n is the total number of observations.
3) Look for the value at (n + 1)/2. Use the result in step 2.
If c contains a fractional half, it means the median is the average of two values. For example, if the location is 3.5, the median is the average of the 3rd and 4th data points.
Illustration
Find the median of each data set.
1) 2, 5, 6, 0, 9, 15, 12
2) 4, 5, 2, 6, 9, 16
Solutions
1) Arrange the data values from least to greatest.
0, 2, 5, 6, 9, 12, 15
Find the middle data point. Since there are seven (odd) observations, the median is the (7+1)/2 = 4th data point. The 4th point is 6 so the median is 6.
2) Arrange the data values from least to greatest.
2, 4, 5, 6, 9, 16
Find the middle data point. Since there are six (even) observations, the median is at (6+1)/2 = 3.5, or the average of the 3rd and 4th data points, (5+6)/2 = 5.5.
Calculator solutions
To find the median, hold the factorial key (n!) and select median. You can also type "median" using the a-z keyboard. Enter the data set in parentheses or in brackets as a matrix.
Examples
1) The test scores (out of 20 points) of 15 students in a Statistics class are: 12, 15, 10, 9, 8, 6, 12, 13, 19, 20, 18, 14, 15, 6, 5.
Find the median of the test scores.
2) The starting monthly salaries of 10 employees at a certain company are listed below.
$1200, $3600, $4500, $3500, $16000, $ 18200, $2500, $10500, $6500, $9650
What is the median starting salary of these employees?
Calculator solutions
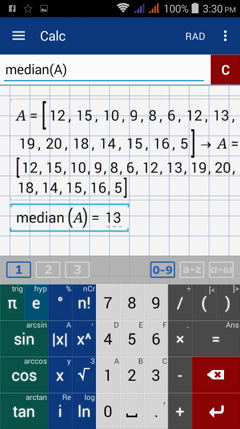
1) Data set: 12, 15, 10, 9, 8, 6, 12, 13, 19, 20, 18, 14, 15, 6, 5
Enter the data set in matrix form and name it using a capital letter.
Enter the data set in brackets.
Separate each data point with a comma.
A = [12, 15, 10, 9, 8, 6, 12, 13, 19, 20, 18, 14, 15, 6, 5]
Hold the factorial key (n!) and select median. Enter matrix A.
Expression syntax: median (A)
1) The test scores (out of 20 points) of 15 students in a Statistics class are: 12, 15, 10, 9, 8, 6, 12, 13, 19, 20, 18, 14, 15, 6, 5.
Find the median of the test scores.
2) The starting monthly salaries of 10 employees at a certain company are listed below.
$1200, $3600, $4500, $3500, $16000, $ 18200, $2500, $10500, $6500, $9650
What is the median starting salary of these employees?
Calculator solutions
1) Data set: 12, 15, 10, 9, 8, 6, 12, 13, 19, 20, 18, 14, 15, 6, 5
Enter the data set in matrix form and name it using a capital letter.
Enter the data set in brackets.
Separate each data point with a comma.
A = [12, 15, 10, 9, 8, 6, 12, 13, 19, 20, 18, 14, 15, 6, 5]
Hold the factorial key (n!) and select median. Enter matrix A.
Expression syntax: median (A)
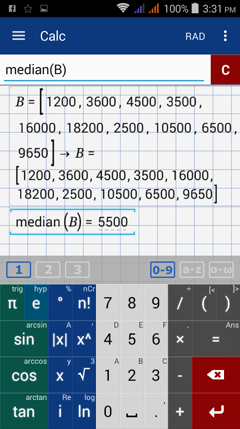
2) Data set: $1200, $3600, $4500, $3500, $16000, $ 18200, $2500, $10500, $6500, $9650
Enter the data set in matrix form and name it using a capital letter.
Enter the data set in brackets.
Separate each data point with a comma.
B = [1200, 3600, 4500, 3500, 16000, 18200, 2500, 10500, 6500, 9650]
Hold the factorial key (n!) and select median. Enter matrix B.
Expression syntax: median (B)