20.3. Digamma Function
The digamma function is defined as the logarithmic derivative of the gamma function. It is denoted by the greek letter "ψ" (psi).
If n is a natural number, the digamma function is defined as: ψ(n) = [ ln (Γ (n) ) ]' = Γ'(z) / Γ(z).
The simplest form of the digamma function is ψ(n) = -(γ + 1/n) + Σ[x=1, ∞] [n/(x² + nx)], where γ is the Euler-Mascheroni constant with a value of 0.57721566490153286060651209. When n is a positive integer, ψ(n) can be evaluated as:
If n is a natural number, the digamma function is defined as: ψ(n) = [ ln (Γ (n) ) ]' = Γ'(z) / Γ(z).
The simplest form of the digamma function is ψ(n) = -(γ + 1/n) + Σ[x=1, ∞] [n/(x² + nx)], where γ is the Euler-Mascheroni constant with a value of 0.57721566490153286060651209. When n is a positive integer, ψ(n) can be evaluated as:
Illustrative Example
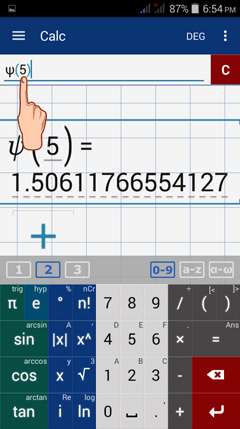
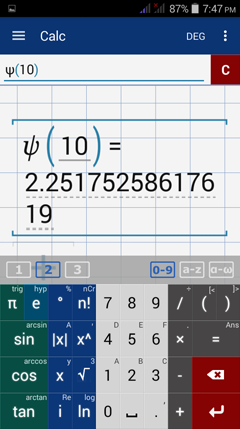
Find the digamma function of 5.
Solution
Since it's easy to make a mistake calculating the digamma function by hand, you can use the app to check your work.
To find the digamma function of a natural number, do the following:
To find the digamma function of a natural number, do the following:
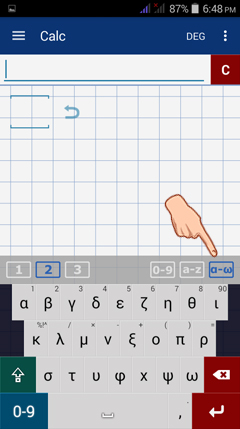
1) Switch to the Greek keyboard by tapping the leftmost keyboard button.
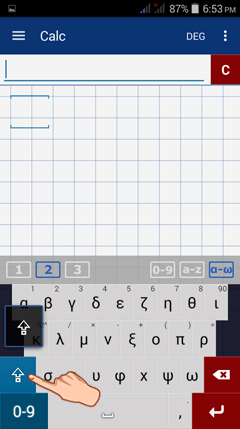
2) Make sure to use the lowercase Greek letters. To switch to lowercase, tap the up-arrow above the 0-9 key.
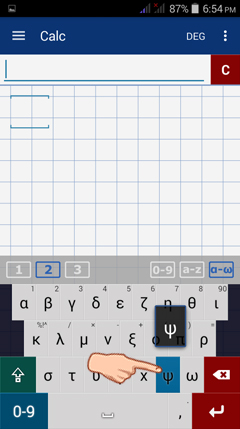
3) Enter ψ (psi) next to ω (omega).
4) Type the number, or argument, in parentheses.
Examples
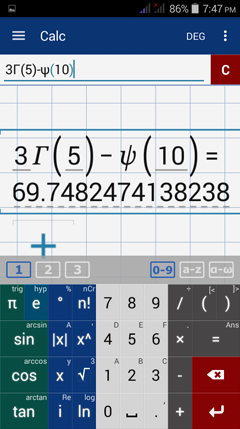
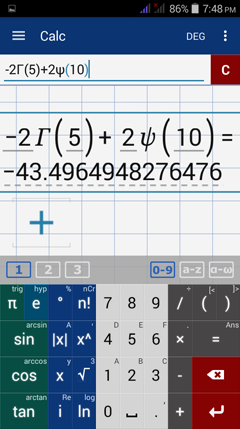
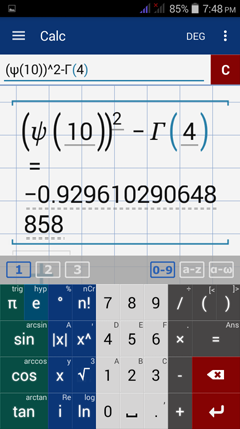
Evaluate each digamma function below.