9.7. Compound Inequalities
Solving a compound inequality means finding values for x that make the inequality true.
Type the inequality as given in the problem with one inequality per line.
Examples
Solve each compound inequality.
Type the inequality as given in the problem with one inequality per line.
Examples
Solve each compound inequality.
1) 2x – 1 < x + 3 < 4
2) 2(x + 1) ≤ 3x – 4 ≥ 2
3) 12 < x – 1 < 15
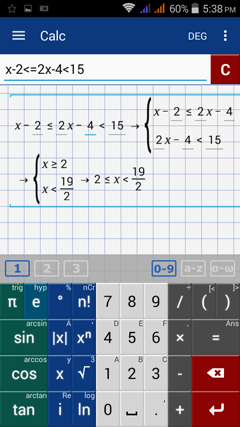
4) x – 2 ≤ 2x – 4 < 15
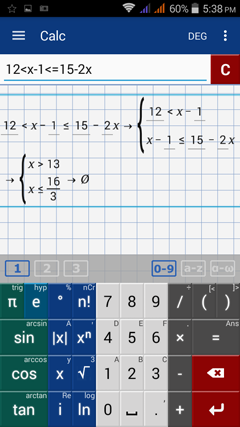
5) 12 < x – 1 ≤ 15 – 2x
2) 2(x + 1) ≤ 3x – 4 ≥ 2
3) 12 < x – 1 < 15
4) x – 2 ≤ 2x – 4 < 15
5) 12 < x – 1 ≤ 15 – 2x
Calculator solutions
Type the less than sign ( < ) by tapping the open parentheses " ( " three times.
Type the greater than sign ( > ) by tapping the closed parentheses " ) " three times.
1) Enter the expression: 2x - 1 < x + 3 < 4.
Type the less than sign ( < ) by tapping the open parentheses " ( " three times.
Type the greater than sign ( > ) by tapping the closed parentheses " ) " three times.
1) Enter the expression: 2x - 1 < x + 3 < 4.
2) Enter the expression: 2(x + 1) < 3x - 4 > 2 by typing "2(x + 1) <= 3x - 4 >= 2."
3) Enter the expression: 12 < x - 1 < 15.
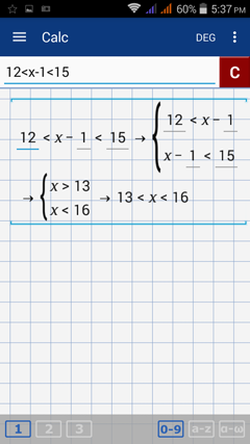
4) Enter the expression: x - 2 < 2x - 4 < 15 by typing "x - 2 <= 2x - 4 < 15."
5) Enter the expression: 12 < x - 1 < 15 - 2x by typing "12 < x - 1 <= 15 - 2x."