6.15. Polar to Rectangular Coordinates
Two most commonly used ways of locating a point in a plane are the polar coordinates and rectangular coordinates.
Rectangular coordinates are denoted by (a, b) where a is the horizontal distance of the point from the origin while b is the vertical distance. Polar coordinates are expressed in the form (r, θ), where r refers to the distance from the origin to the point and θ refers to the degree measure of the angle formed between the positive x-axis and the vector (connecting the origin and the point).
In the previous section, we denote a = r cos θ theta and b = r sin θ. Manually, we use these two formulas to convert the polar coordinates of a point into its equivalent rectangular form.
Illustrative Example
A point has coordinates (3, 40°). What are its coordinates in rectangular form?
Manual Solution
Find the horizontal distance a using the formula: a = r cos θ
a = 3 cos 40° ≈ 2.298133
Find the vertical distance b using the formula: b = r sin θ
b = 3 sin 40° ≈ 1.928363
The rectangular coordinates of the point are (2.298133, 1.928363).
Calculator Solution
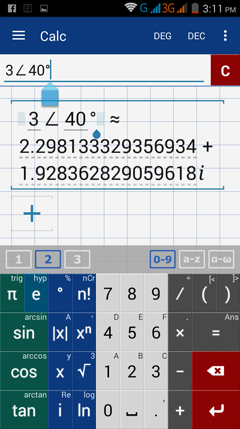
Enter the polar coordinates using the format: r ∠ θ.
The equivalent rectangular coordinates are automatically displayed on your screen in the form: a + bi
Note: In case, your calculator doesn't display the result in a + bi form, just tap the "number format" button on the upper right of your screen. Set number format to any of the available formats except AUTO.
Rectangular coordinates are denoted by (a, b) where a is the horizontal distance of the point from the origin while b is the vertical distance. Polar coordinates are expressed in the form (r, θ), where r refers to the distance from the origin to the point and θ refers to the degree measure of the angle formed between the positive x-axis and the vector (connecting the origin and the point).
In the previous section, we denote a = r cos θ theta and b = r sin θ. Manually, we use these two formulas to convert the polar coordinates of a point into its equivalent rectangular form.
Illustrative Example
A point has coordinates (3, 40°). What are its coordinates in rectangular form?
Manual Solution
Find the horizontal distance a using the formula: a = r cos θ
a = 3 cos 40° ≈ 2.298133
Find the vertical distance b using the formula: b = r sin θ
b = 3 sin 40° ≈ 1.928363
The rectangular coordinates of the point are (2.298133, 1.928363).
Calculator Solution
Enter the polar coordinates using the format: r ∠ θ.
The equivalent rectangular coordinates are automatically displayed on your screen in the form: a + bi
Note: In case, your calculator doesn't display the result in a + bi form, just tap the "number format" button on the upper right of your screen. Set number format to any of the available formats except AUTO.
More Examples
A point has the following polar coordinates. Convert these coordinates to rectangular form.
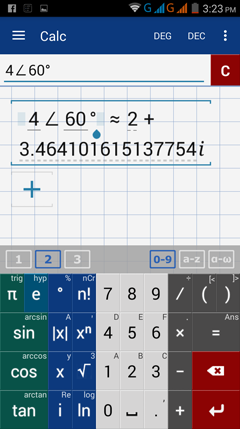
1) (4, 60°)
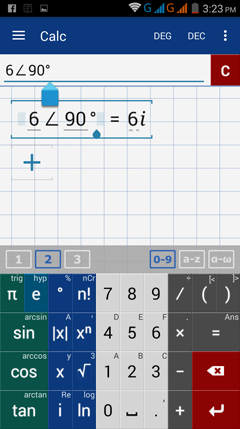
2) (6, 90°)
3) (2, 45°)
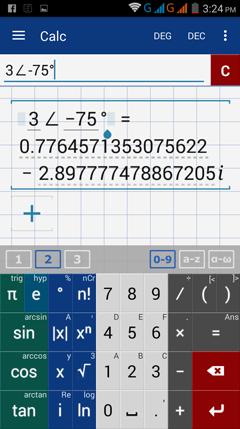
4) (3, -75°)
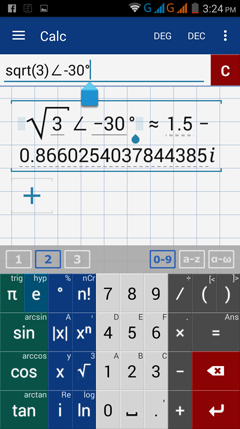
5) (sqrt (3), -30°)
Calculator Solutions
1) Enter: 4 ∠ 60°
2) Enter: 6 ∠ 90°
3) Enter: 2 ∠ 45°
4) Enter: 3 ∠ -75°
5) Enter: sqrt(3) ∠ -30°