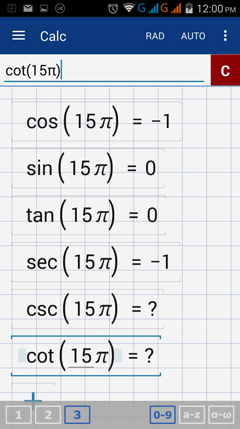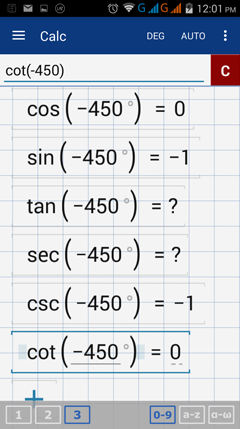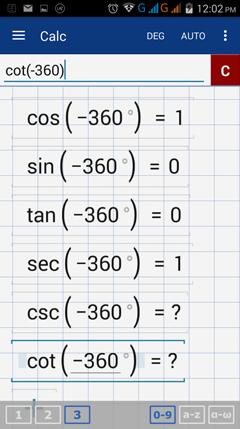13.3.3. Quadrantal Angles
An angle whose terminal side coincides with either x or y axis is called a quadrantal angle. Quadrantal angles are measured in 90° increment such as 90°, 180°, 270°, 360°, and so on. In radians, quadrantal angles are measured in π increments (π , 2π , 3π , 4π , 5π, etc.) Calculation of the exact value of the six trigonometric ratios of any quadrantal angle is based from the following:
cos 90° = 0
sec 90° = undefined
sin 90° = 1
csc 90° = 1
tan 90° = undefined
cot 90° = 0
Note: The question mark result displayed in the calculator means the function value is not defined. Depending on which axis does the terminal side of a quadrantal angle lie, the signs of these values would vary. Likewise, the cosine and sine values would
interchange.
Now, let us find the values of the six trigonometric ratios of some quadrantal angles.
Examples
Find the values of the six trigonometric ratios for each angle below.
1) 180°
2) 15π
3) -450°
4) -360°
5) -8π
Calculator Solutions
Input each ratio using the trigonometric keys.
Enter one ratio per line.
Add the degree symbol if the given angle is measured in degrees.
Otherwise, tap the DEG button to swift to RAD and add the π symbol.
1) Trigonometric function values of 180°
Note: The terminal side of a 180° angle lies in the negative x-axis so cosine and sine values are negative.
2) Trigonometric function values of 15π
3) Trigonometric function values of - 450°
4) Trigonometric function values of -360°
5) Trigonometric function values of -8π