16.6. Derivative of Rational Functions
Finding the derivative of a rational function involves relying on the quotient rule. To make it easier, first simplify the rational expression if possible.
Enter the numerator and denominator in parentheses and place the entire rational expression in another set of parentheses. Tap the exponent key (x^) twice to take the first derivative and three times to take the second derivative. To find the third derivative, take the first derivative of the second derivative.
Examples
Find the derivative of each rational function below.
Enter the numerator and denominator in parentheses and place the entire rational expression in another set of parentheses. Tap the exponent key (x^) twice to take the first derivative and three times to take the second derivative. To find the third derivative, take the first derivative of the second derivative.
Examples
Find the derivative of each rational function below.
Calculator solutions
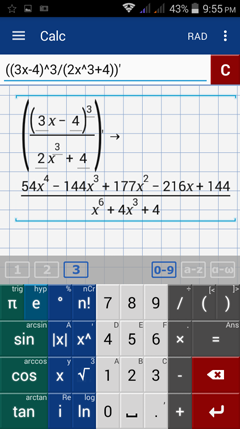
Enter each expression as given. Type the expression in parentheses and take the first derivative by tapping the exponent key (x^n) twice.
1) Type: ((3x - 4)^3/(2x^3 + 4))'
Enter each expression as given. Type the expression in parentheses and take the first derivative by tapping the exponent key (x^n) twice.
1) Type: ((3x - 4)^3/(2x^3 + 4))'
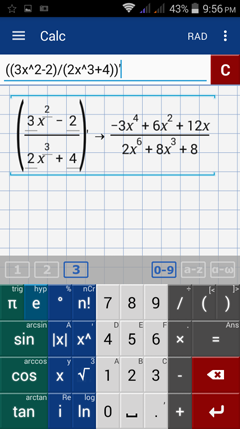
2) Type: ((3x^2 - 2)/(2x^3 + 4))'
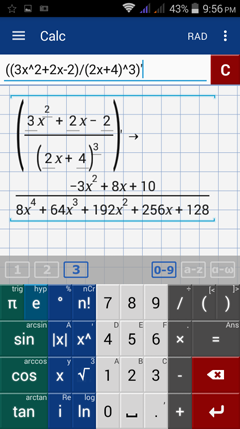
3) Type: ((3x^2 + 2x - 2)/(2x + 4)^3)'