7.3. Absolute Values
Absolute Value Key | x |
Other keys available on this button are: norm, det, tr, adj, ^ T
Use |x| to enter expressions that involve an absolute value such as | -2 |, | -2 + 4(-3) | and | -2x +3 | = 5. Tap the absolute value key and then enter the argument. If the argument includes multiple terms, enclose them in parentheses.
Note: This function also computes the distance from 0 for complex numbers.
Examples
Simplify the following.
Other keys available on this button are: norm, det, tr, adj, ^ T
Use |x| to enter expressions that involve an absolute value such as | -2 |, | -2 + 4(-3) | and | -2x +3 | = 5. Tap the absolute value key and then enter the argument. If the argument includes multiple terms, enclose them in parentheses.
Note: This function also computes the distance from 0 for complex numbers.
Examples
Simplify the following.
1. | -2 |
2. | -2 + 5(-3) |
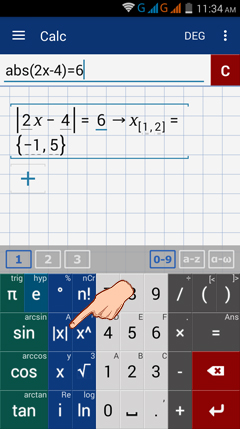
3. | 2x – 4 | = 6
Calculator solutions
Enter each expression as given with one expression per line. Use the absolute value key |x| before entering an argument.
1) Use |x| then enter: (-2)
2) Use |x| then enter: (-2+5(-3))
3) Use |x| then enter: (2x-4) = 6
Enter each expression as given with one expression per line. Use the absolute value key |x| before entering an argument.
1) Use |x| then enter: (-2)
2) Use |x| then enter: (-2+5(-3))
3) Use |x| then enter: (2x-4) = 6
Norm Key
Norm refers to the magnitude or length of a vector on a vector space. To use the norm command, tap the absolute value key |x| twice. Enclose the arguments in brackets and use the space bar to separate terms.
Norm refers to the magnitude or length of a vector on a vector space. To use the norm command, tap the absolute value key |x| twice. Enclose the arguments in brackets and use the space bar to separate terms.