6.14. The Polar Form of Complex Numbers
In the previous section, we defined the set of complex numbers as the set of real and imaginary numbers. Most of us, if not all, are familiar about complex numbers in the form a + bi, where a represents the real number part and bi represents the imaginary number part. Complex numbers can also be written in several forms, polar form, to name one.
Any complex number in the form a + bi can be thought of as a vector that starts from the origin to a point (a, b) in the standard coordinate system or as a point (a, b) in the XY-plane, which in this context, is appropriately called as the complex plane. In the complex plane, the x-axis is called the real axis and the y-axis as the imaginary axis.
To establish a relationship between these two interpretations, let us consider complex number z = a + b i. This complex number z can be thought of as the length of the vector calculated as sqrt (a^2 + b^2). Likewise, z = a + b i, a non-zero complex number can be thought of as a point (a, b ) where a = r cos θ and b = r sin θ. Furthermore, this point (a, b) can also be represented in polar form (r, θ) where r is equal to the absolute value of z. These interpretations would now lead us to the following conversion formulas, given z = a + bi.
a = r cos θ b = r sin θ θ = arc tan (b / a)
In this section, we will first deal with the polar form of complex numbers. The succeeding examples illustrate the conversion of the standard complex number z = a + bi to its equivalent polar form (r, θ).
Note: This calculator displays (r, θ) into the form: r ∠ θ
To convert complex number to its polar form, follow the general steps below:
1) Enter the complex number using the format: z = a + bi
2) Then, enter the conversion command: abs(z) ∠ arg(z)
Hold i key to see arg and ∠ keys.
In case, your calculator doesn't display the result in polar form, just tap the number format button on the upper right (beside DEG - RAD) button. Make sure to set it to AUTO.
Note: This calculator displays (r, θ) into the form: r ∠ θ
To convert complex number to its polar form, follow the general steps below:
1) Enter the complex number using the format: z = a + bi
2) Then, enter the conversion command: abs(z) ∠ arg(z)
Hold i key to see arg and ∠ keys.
In case, your calculator doesn't display the result in polar form, just tap the number format button on the upper right (beside DEG - RAD) button. Make sure to set it to AUTO.
Illustrative Example
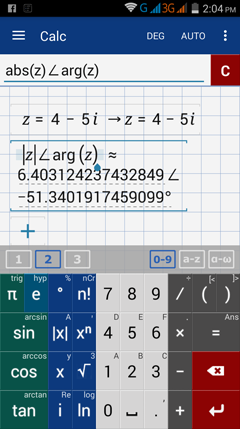
Convert 4 - 5 i to polar form.
Manual Solution
Step 1: Find the value of r using the formula: z = sqrt (a^2 + b^2).
Step 2: Find the value of θ.
Therefore, 4 - 5 i is written as (6.4031242, -51.34019°) in polar form.
Calculator Solution
Step 1: Enter: z = 4 - 5 i
Step 2: Enter: abs (z) ∠ arg(z)
Hold i key to use arg and ∠ keys.
More Examples
Convert each complex number number below to its polar form.
Calculator Solutions
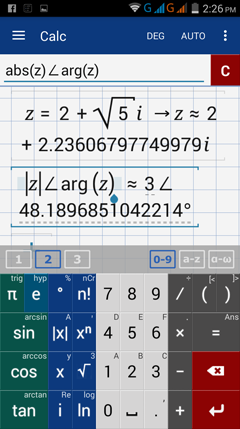
1) Enter: z = 2 + sqrt(5) i
Enter: abs (z) ∠ arg(z)
Enter: abs (z) ∠ arg(z)
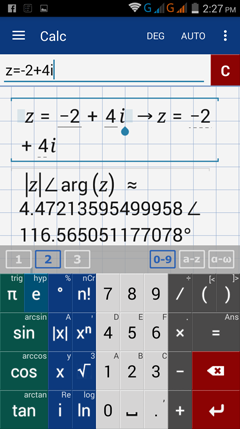
2) Enter: z = -2 + 4 i
Enter: abs (z) ∠ arg(z)
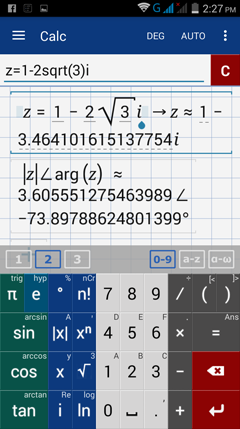
3) Enter: z = 1 - 2 sqrt(3) i
Enter: abs (z) ∠ arg(z)
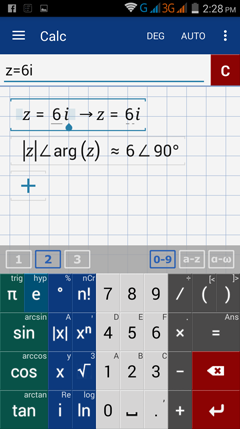
4) Enter: z = 6i
Enter: abs (z) ∠ arg(z)
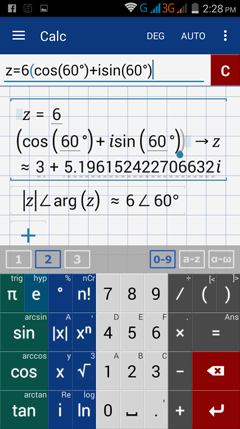
5) Enter: z = 6( cos 60° + i sin 60°)
Enter: abs (z) ∠ arg(z)