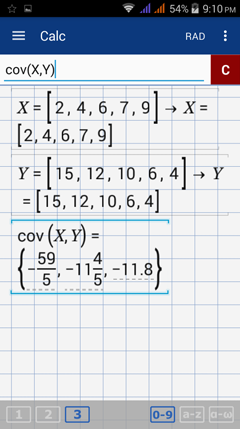19.8.1. Covariance
Covariance measures how two variables change together and it considers the variability of both data sets, X and Y. It helps us determine whether a greater variability in X could result in an even greater variability in Y or the other way around. The sign of the covariance shows us this relationship. When the value is positive, both variables increase or decrease together. When it's negative, the variables move in opposite directions. To calculate the covariance, we take the average of the products of the deviations in X and Y such that
|
where:
cov (X, Y) - covariance of the sample x - data value in X x̄ - mean of X y - data value in Y ȳ - mean of Y n - number of data pairs |
or
|
where:
cov (X, Y) - covariance for population data sets X - data value in X μ (x) - mean of X Y - data value in Y μ (y) - mean of Y N - number of data pairs |
Calculating the Variance
To find the covariance of a paired data set, use the following steps:
1) Find the mean of the values of the independent variable X.
2) Find the mean of the values of the dependent variable Y.
3) Find the deviations in X by subtracting the mean of X from each X value and the deviations in Y by subtracting the mean of Y from each Y value.
4) Multiply the respective results from steps 3 and 4.
5) Find the average of the results from step 5. This average is the value of the covariance.
Illustrative Example
Calculate the covariance of the given bivariate data set.
X Y
2 15
4 12
6 10
7 6
9 4
Solution
1) Find the mean of X.
Mean (X) = (2 + 4 + 6 + 7 + 9) / 5 = 5.6
2) Find the mean of Y.
Mean (Y) = (15 + 12 + 10 + 6 + 4) /5 = 9.4
3) Find the deviations in X and Y.
X Y X - Mean(X) Y - Mean (Y)
2 15 - 3.6 5.6
4 12 - 1.6 2.6
6 10 0.4 0.6
7 6 1.4 -3.4
9 4 3.4 - 5.4
4) Find the product of the deviations in X and Y.
X Y X - Mean(X) Y - Mean (Y) (X - Mean(X))(Y - Mean(Y))
2 15 - 3.6 5.6 - 20.16
4 12 - 1.6 2.6 - 4.16
6 10 0.4 0.6 0.24
7 6 1.4 -3.4 -4.76
9 4 3.4 - 5.4 -18.36
5) Find the average of the products obtained from step 4.
Covariance (p) = (-20.16 + -4.16 + 0.24 + -4.76 + -18.36) / 5 = - 9.44 (if the data set represents a population of values)
Covariance = = (-20.16 + -4.16 + 0.24 + -4.76 + -18.36) / 4 = - 11.8 (if the data set represents sample of values)
The negative covariance implies an inverse relationship between X and Y.
COV and COVP Keys
To find a covariance using the app, use the cov and covp functions by holding the factorial (n!) key and selecting "cov" or "covp" respectively. "cov" is used to find the covariance of a sample while "covp" is used to find the covariance of a population.
To calculate the covariance, use the following steps:
1) Enter the data sets in matrix form. Enter the values for X in one matrix and the values of Y in another matrix.
Use different names for these matrices, X and Y for example.
Note: Matrices X and Y must have the same length.
X = [2, 4, 6, 7, 9]
Y = [15, 12, 10, 6, 4]
2) Hold the factorial (n!) key and select cov (for a sample) or covp (for a population).
3) Enter the names of the matrix in the order: cov (X, Y) or covp (X, Y).
Example
Using the same data set, calculate the covariance using the "cov" or "covp" key, whichever is appropriate.
X = [2, 4, 6, 7, 9]
Y = [15, 12, 10, 6, 4]
To find a covariance using the app, use the cov and covp functions by holding the factorial (n!) key and selecting "cov" or "covp" respectively. "cov" is used to find the covariance of a sample while "covp" is used to find the covariance of a population.
To calculate the covariance, use the following steps:
1) Enter the data sets in matrix form. Enter the values for X in one matrix and the values of Y in another matrix.
Use different names for these matrices, X and Y for example.
Note: Matrices X and Y must have the same length.
X = [2, 4, 6, 7, 9]
Y = [15, 12, 10, 6, 4]
2) Hold the factorial (n!) key and select cov (for a sample) or covp (for a population).
3) Enter the names of the matrix in the order: cov (X, Y) or covp (X, Y).
Example
Using the same data set, calculate the covariance using the "cov" or "covp" key, whichever is appropriate.
X = [2, 4, 6, 7, 9]
Y = [15, 12, 10, 6, 4]
