6.7.4. Fractional Part of a Number
In a number n, the integer (or integral) part of a number is the largest integer that is not greater than n. The fractional part is the difference between the integer part and n. For example, the number 3.5 has an integer part of 3 and a fractional part of 0.5.
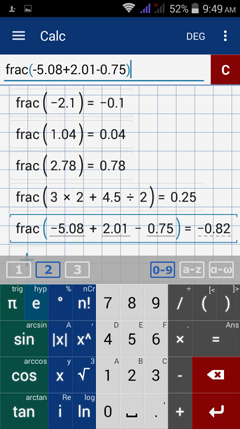
To find the fractional part of a number or result, type in frac(x) and enclose the term in parentheses.
Examples
Find the fractional part of each number or result.
1) -2.1
2) 1.04
3) 2.78
4) 3 × 2 + 4.5 ÷ 2
5) (-5.08 + 2.01 – 0.75)
Solutions
Make sure that the number format is set to Auto. Type "frac" before each argument.
1) frac(-2.1)
2) frac(1.04)
3) frac(2.78)
4) frac(3 × 2 + 4.5 ÷ 2)
5) frac(-5.08 + 2.01 – 0.75)
To find the fractional part of a number or result, type in frac(x) and enclose the term in parentheses.
Examples
Find the fractional part of each number or result.
1) -2.1
2) 1.04
3) 2.78
4) 3 × 2 + 4.5 ÷ 2
5) (-5.08 + 2.01 – 0.75)
Solutions
Make sure that the number format is set to Auto. Type "frac" before each argument.
1) frac(-2.1)
2) frac(1.04)
3) frac(2.78)
4) frac(3 × 2 + 4.5 ÷ 2)
5) frac(-5.08 + 2.01 – 0.75)