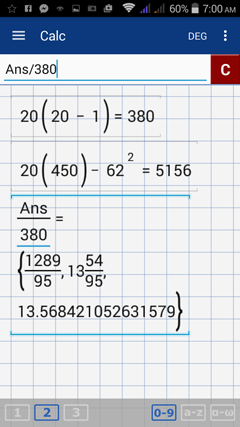1.7. Using the Last Answer
Some problems become easier when the operations are broken down into simpler steps. The equal or answers key can be used to perform these operations in succession.
After performing one calculation, tap the "=' key twice to use the answer from the previous operations. Note that ANS (answer) is then displayed in the input field, meaning that the current calculation is using the final answer from the previous equation or expression.
Example
Simplify the expression below:
Simplify the expression below:
This expression can be solved directly on the graphing calculator but it requires many grouping symbols. Instead of having to enter several sets of parentheses, it may be easier to perform multiple operations by using the last answer to carry over your results.
The following steps will illustrate how this expression may be broken down:
Step 1:
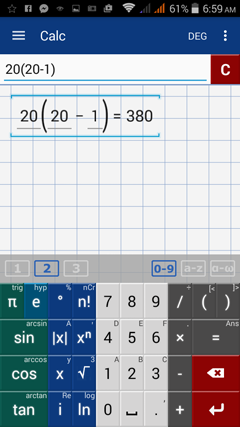
Simplify the denominator: 20(20 – 1).
Calculator solution
Enter the expression: 20(20 – 1)
The following steps will illustrate how this expression may be broken down:
Step 1:
Simplify the denominator: 20(20 – 1).
Calculator solution
Enter the expression: 20(20 – 1)
Step 2
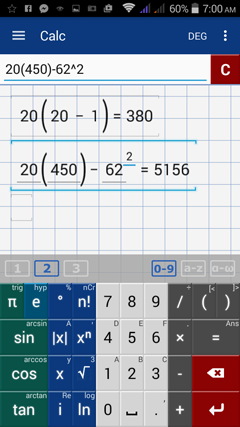
Calculate the numerator: 20(450) - 62^2
Calculator solution
Enter the expression: 20(450) - 62^2
Calculate the numerator: 20(450) - 62^2
Calculator solution
Enter the expression: 20(450) - 62^2
Step 3:
Divide the answer found in Step 2 by the answer found in Step 1.
Calculator solution
Double tap the = key, /, then type 380 (the answer found in Step 1).
Divide the answer found in Step 2 by the answer found in Step 1.
Calculator solution
Double tap the = key, /, then type 380 (the answer found in Step 1).
Step 4:
Take the square root of the answer found in Step 3.
Calculator solution
Enter the root key and tap "=" twice.
Take the square root of the answer found in Step 3.
Calculator solution
Enter the root key and tap "=" twice.
One-Step Calculator Solution
Enter the expression as it appears in the problem by using the root key and typing the argument in parentheses as shown below.
Enter the expression as it appears in the problem by using the root key and typing the argument in parentheses as shown below.