6.9. Least Common Multiple
The least common multiple (LCM) of two or more numbers is the smallest positive number that is divisible by each of the given numbers. To find the LCM of two numbers, type lcm(a,b) where a and b are the two numbers.
Examples
Find the least common multiple of the given sets of numbers.
1) 12, 30
2) 5, 12
3) 20, 40
4) 35, 45, 50
5) 20, 25, 30
Calculator Solutions
Type "lcm" before each pair of arguments and separate them with a comma.
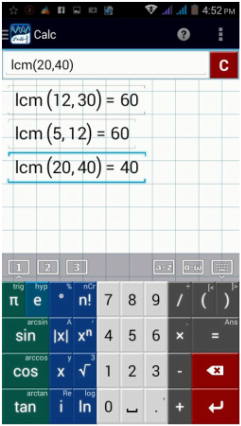
1) lcm(12, 30). The lcm is 60.
2) lcm(5, 12). The lcm is 60.
3) lcm(20, 40). The lcm is 40.
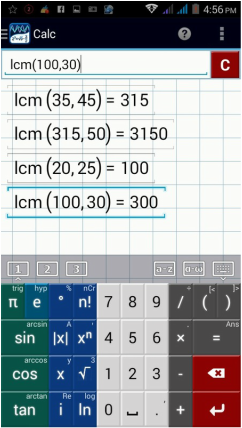
4) Find the lcm between 35 and 45. Then pair the lcm with 50.
lcm(35, 45). The lcm is 315.
lcm(315, 50). The lcm is 3150.
5) Find the lcm between 20 and 25. Then pair the lcm with 30.
lcm(20, 25). The lcm is 100.
lcm(100, 30). The lcm is 300.
Note: To find the lcm of more than 3 numbers, find the lcm of two numbers at a time. First, find the lcm of the first two numbers, then the last two. Then find the lcm of the lcm of the two sets of numbers.
i.e. lcm(a,b) = E
lcm(c,d) = F
lcm(E,F) = G Final Answer
Apply the same steps for more than 4 given numbers.
Examples
Find the least common multiple of the given sets of numbers.
1) 12, 30
2) 5, 12
3) 20, 40
4) 35, 45, 50
5) 20, 25, 30
Calculator Solutions
Type "lcm" before each pair of arguments and separate them with a comma.
1) lcm(12, 30). The lcm is 60.
2) lcm(5, 12). The lcm is 60.
3) lcm(20, 40). The lcm is 40.
4) Find the lcm between 35 and 45. Then pair the lcm with 50.
lcm(35, 45). The lcm is 315.
lcm(315, 50). The lcm is 3150.
5) Find the lcm between 20 and 25. Then pair the lcm with 30.
lcm(20, 25). The lcm is 100.
lcm(100, 30). The lcm is 300.
Note: To find the lcm of more than 3 numbers, find the lcm of two numbers at a time. First, find the lcm of the first two numbers, then the last two. Then find the lcm of the lcm of the two sets of numbers.
i.e. lcm(a,b) = E
lcm(c,d) = F
lcm(E,F) = G Final Answer
Apply the same steps for more than 4 given numbers.