11.6. Quadratic Functions
A quadratic function can be written in (1) the general form f(x) = ax^2 + bx + c where a, b, and c are real numbers or (2) the vertex form f(x) = a(x - h)^2 + k where a corresponds to the direction and span of the graph and (h, k) is the vertex.
The graph of a quadratic function is a parabola. The line that divides the parabola into two equal parts is the axis of symmetry which passes through the parabola's vertex. The vertex is a maximum or minimum of the parabola depending on whether the graph of the parabola points up or down.
If there are any restrictions, you can also set a domain for the quadratic function.
Examples
Sketch the graph of the following quadratic functions and note their properties.
1) f(x) = 3x^2 - 4x + 1
2) f(x) = 6(x - 2)^2
3) f(x) = 3(x + 1)^2 - 5
4) f(x) = -3(x - 1)^2 + 1
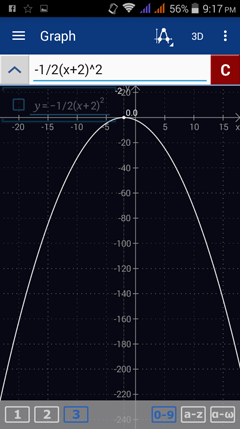
5) f(x) = - 1/2 (x + 2)^2
Solutions
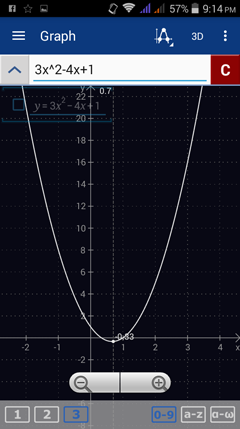
1) f(x) = 3x^2 - 4x + 1
Enter the expression: 3x^2 - 4x + 1
The graph of a quadratic function is a parabola. The line that divides the parabola into two equal parts is the axis of symmetry which passes through the parabola's vertex. The vertex is a maximum or minimum of the parabola depending on whether the graph of the parabola points up or down.
If there are any restrictions, you can also set a domain for the quadratic function.
Examples
Sketch the graph of the following quadratic functions and note their properties.
1) f(x) = 3x^2 - 4x + 1
2) f(x) = 6(x - 2)^2
3) f(x) = 3(x + 1)^2 - 5
4) f(x) = -3(x - 1)^2 + 1
5) f(x) = - 1/2 (x + 2)^2
Solutions
1) f(x) = 3x^2 - 4x + 1
Enter the expression: 3x^2 - 4x + 1
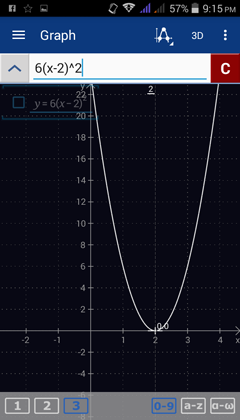
2) f(x) = 6(x - 2)^2
Enter the expression: 6(x - 2)^2
Enter the expression: 6(x - 2)^2
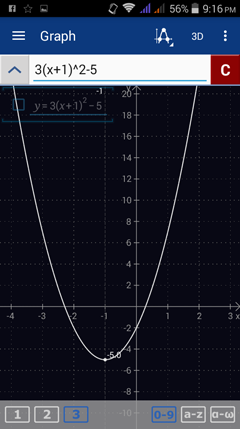
3) f(x) = 3(x + 1)^2 - 5
Enter the expression: 3(x + 1)^2 - 5
Enter the expression: 3(x + 1)^2 - 5
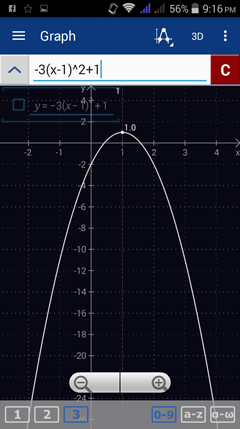
4) f(x) = -3(x - 1)^2 + 1
Enter the expression: -3(x - 1)^2 + 1
Enter the expression: -3(x - 1)^2 + 1
5) f(x) = - 1/2 (x + 2)^2
Enter the expression: -1/2 (x + 2)^2
Enter the expression: -1/2 (x + 2)^2