16.4. Rules of Differentiation

There are certain rules you can use to find a derivative.
1) The derivative of a constant is zero.
2) Power rule
     The derivative of x^n is nx^(n-1)
3) Addition rule
    (f + g)' = f ' + g'
4) Subtraction rule
    (f - g)' = f ' - g'
5) Derivative of a constant product where c is a constant and y is a variable
    (cy) ' = c*y'
6) Product rule
     [f(x) * g(x)]' = f '(x) * g(x) + f(x) * g'(x)
7) Quotient rule
    [f(x) / g(x)]' = [f '(x) * g(x) - f (x) * g'(x)] / (g(x))^2
8) Chain rule
     [f(g(x))]' = f '(g(x)) * g'(x)

Examples
Find the derivative of each function below.
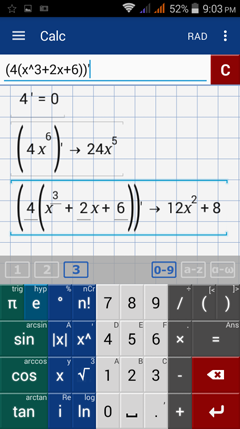
1) f(x) = 4
2) f(x) = 4x^6
3) f(x) = 4(x^3 + 2x + 6)
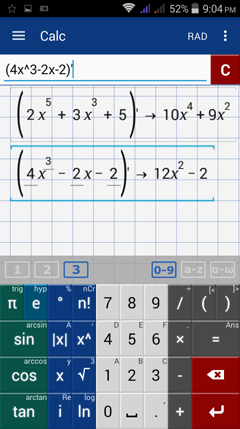
4) h(x) = 2x^5 + 3x^3 + 5
5) g(x) = 4x^3 - 2x - 2
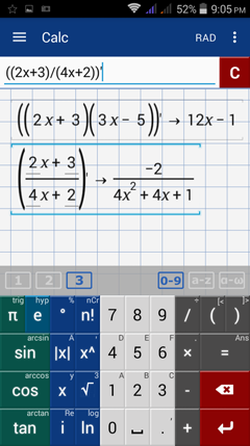
6) f(x) = (2x + 3)(3x - 5)
7) g(x) = (2x + 3) / (4x + 2)
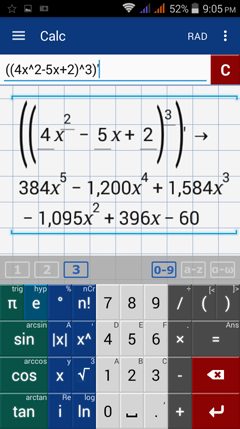
8) h(x) = (4x^2 - 5x + 2)^3

Calculator solutions
Enter the expression of each equation as given. Enter it in parentheses and tap the exponent key (x^n) twice to take the derivative.
1) Type: 4'
2) Type: (4x^6)'
​3) Type: (4(x^3 + 2x + 6))'

4) Type: (​2x^5 + 3x^3 + 5)'
​5) Type: (4x^3 - 2x - 2)'

6) Type: ((2x + 3)(3x - 5))'
7) Type: ((2x + 3) / (4x + 2))'

---

8) Type: ((4x^2 - 5x + 2)^3)'

NEXT: 16.5. DERIVATIVES OF POLYNOMIAL FUNCTIONS >

list of contents