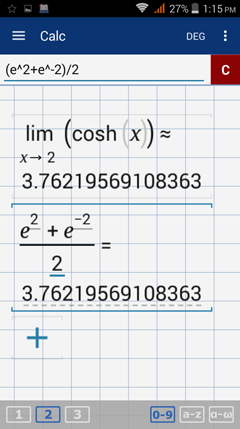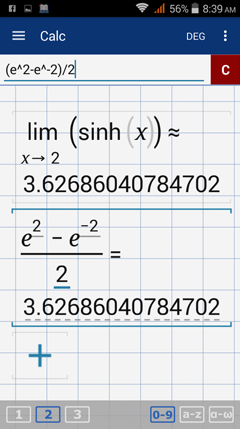15.13. Limit of a Hyperbolic Function
A hyperbolic function are analogous to trigonometric functions but refer to base e. Below are six hyperbolic functions derived from the basic definitions of sinhx and coshx.
Calculating the limit of a hyperbolic function involves evaluating a function in terms of e^x and e^(-x) as x approaches c. Like other functions, it can be found by substituting x = c, but it is similarly possible that the limit may not exist.
Illustrative Examples
Calculate each limit if it exists.
Calculate each limit if it exists.
Calculator solution
The limit of cosh x as x approaches 2 is the value of f(2) = e^x + e^(-x))/2.
Type in: lim [ x = 2 ] cosh x
The limit of cosh x as x approaches 2 is the value of f(2) = e^x + e^(-x))/2.
Type in: lim [ x = 2 ] cosh x
Calculator solution
The limit of sinh x as x approaches 2 is the value of f(2) = (e^x - e^(-x))/2.
Type in: lim [ x = 2 ] sinh x
The limit of sinh x as x approaches 2 is the value of f(2) = (e^x - e^(-x))/2.
Type in: lim [ x = 2 ] sinh x
More Examples
Calculate each limit, if it exists.
Calculate each limit, if it exists.
Calculator solution
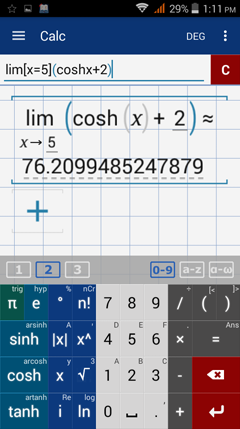
Type in: lim [ x = 5 ] ( cosh x + 2 )
Type in: lim [ x = 5 ] ( cosh x + 2 )
Calculator solution
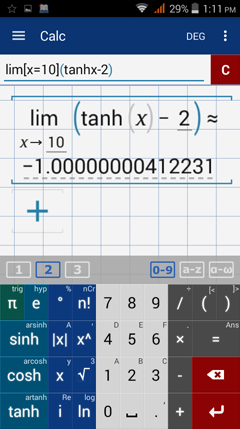
Type in: lim [ x = 10 ] ( tanh x - 2 )
Type in: lim [ x = 10 ] ( tanh x - 2 )
Calculator solution
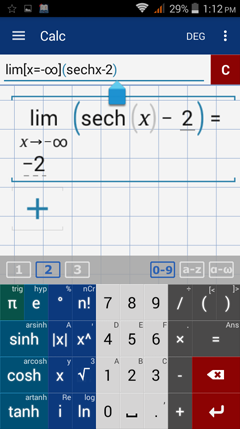
Type in: lim [ x = -∞ ] ( sech x - 2 )
Type in: lim [ x = -∞ ] ( sech x - 2 )
Calculator solution
Type in: lim [ x = ∞ ] cosh x
Type in: lim [ x = ∞ ] cosh x
Calculator solution
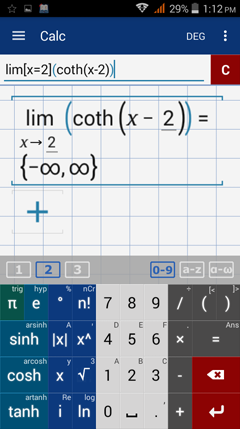
Type in: lim [ x = 2 ] coth ( x -2 )
Type in: lim [ x = 2 ] coth ( x -2 )