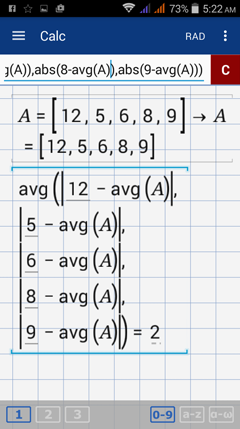19.6.3. Mean Absolute Deviation
The mean absolute deviation (MAD) refers to the average of the absolute differences between each data value and the mean, giving us the average amount of spread relative to the mean.
To find the MAD:
1) Find the mean of the data set.
2) Subtract the mean from each data value.
3) Take the absolute value of the difference.
4) Take the average of all of the absolute differences.
Illustrative Example
What is the mean absolute deviation of the data set below?
12, 5, 6, 8, 9
Solution
1) Find the average of the data values.
Average = (12 + 5 + 6 + 8 + 9)/5 = 8
2) Subtract the mean from each data value.
X X - Mean
12 12-8 = 4
5 5-8 = -3
6 6-8 = -2
8 8-8 = 0
9 9-8 = 1
3) Take the absolute value each difference.
X X - Mean /X - Mean/
12 4 4
5 -3 3
6 -2 2
8 0 0
9 1 1
4) Find the average of the absolute differences.
Average = MAD = (4 + 3 + 2 + 0 + 1)/5 = 2
Relative to the mean, the data set varies by the an average of 2 units.
Although calculating the MAD is simple for small data sets, it's easier to use the app for data sets that are large.
To find the MAD using the app:
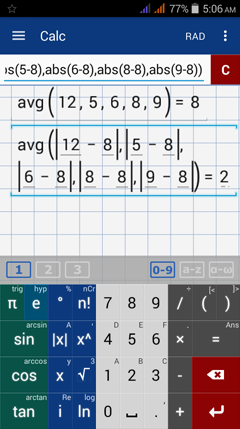
1) Find the average of the data set by using "avg"
avg(12, 5, 6, 8, 9)
2) Find the average of the absolute differences using the "avg" key and entering the absolute differences as data points.
avg(/12 - 8/, /5 - 8/, /6-8/, /8-8/, /9 - 8/)
See the reference below.
Note: You can also enter the data set as a matrix and naming it matrix A, for example. Then enter avg(A) instead of 8 in this case.
1) Find the mean of the data set.
2) Subtract the mean from each data value.
3) Take the absolute value of the difference.
4) Take the average of all of the absolute differences.
Illustrative Example
What is the mean absolute deviation of the data set below?
12, 5, 6, 8, 9
Solution
1) Find the average of the data values.
Average = (12 + 5 + 6 + 8 + 9)/5 = 8
2) Subtract the mean from each data value.
X X - Mean
12 12-8 = 4
5 5-8 = -3
6 6-8 = -2
8 8-8 = 0
9 9-8 = 1
3) Take the absolute value each difference.
X X - Mean /X - Mean/
12 4 4
5 -3 3
6 -2 2
8 0 0
9 1 1
4) Find the average of the absolute differences.
Average = MAD = (4 + 3 + 2 + 0 + 1)/5 = 2
Relative to the mean, the data set varies by the an average of 2 units.
Although calculating the MAD is simple for small data sets, it's easier to use the app for data sets that are large.
To find the MAD using the app:
1) Find the average of the data set by using "avg"
avg(12, 5, 6, 8, 9)
2) Find the average of the absolute differences using the "avg" key and entering the absolute differences as data points.
avg(/12 - 8/, /5 - 8/, /6-8/, /8-8/, /9 - 8/)
See the reference below.
Note: You can also enter the data set as a matrix and naming it matrix A, for example. Then enter avg(A) instead of 8 in this case.
Examples
Find the mean absolute deviation each data set below.
1) 5, 6, 7, 8, 9, 10
2) 0.25, 1.45, 6.75, 9.2, 11.5
Calculator solutions
1) Find the average of the data set using avg. Type in: avg(5, 6, 7, 8, 9, 10). The average is 7.5.
Find the average of the absolute differences by entering: avg (/5 - 7.5/, /6 - 7.5/, /7 - 7.5/, /8 - 7.5/, /9 - 7.5/, /10 - 7.5/)
2) Find the average of the data set using avg. Type in: avg(0.25, 1.45, 6.75, 9.2, 11.5). The average is 5.83.
Find the average of the absolute differences by entering: avg (/0.25 - 5.83/, /1.45 - 5.83/, /6.75 - 5.83/, /9.2 - 5.83/, /11.5 - 5.83/).