17.2. Derivative of a Function df (or dy)
The derivative of a function f(x) is written as f '(x) but it can also be denoted by "dy" or "df." The derivative of the independent variable x is denoted by "dx."
Finding dy where y = f(x)
To find the derivative of a function dy or df is like finding the product of the derivative of the function and Δx. Note that the variable y refers to the dependent variable of f(x).
Illustrative Example
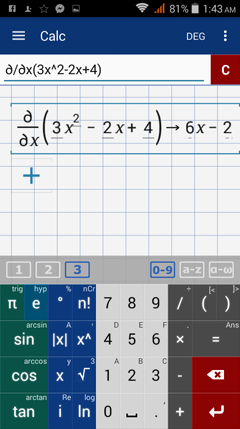
Given f(x) = 3x^2 - 2x + 4, find dy (or df).
Solution
dy = df = f ' (x) dx
dy = (3x^2 - 2x + 4) dx
dy = (6x - 2) dx
Calculator solution
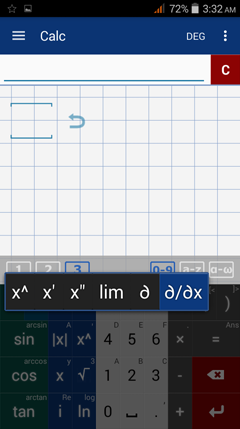
The syntax for df is a function of the exponent key (x^). To use df, tap and hold the exponent key and select the partial derivative:
Illustrative Example
Given f(x) = 3x^2 - 2x + 4, find dy (or df).
Solution
dy = df = f ' (x) dx
dy = (3x^2 - 2x + 4) dx
dy = (6x - 2) dx
Calculator solution
The syntax for df is a function of the exponent key (x^). To use df, tap and hold the exponent key and select the partial derivative:
You can also tap the exponent key (x^) six times to enter a partial derivative.
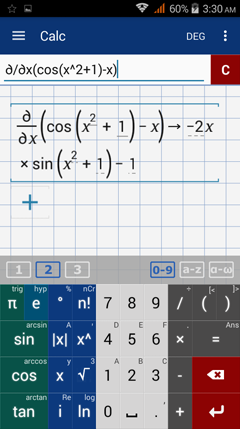
3) Type in the given expression for f(x) next to the partial derivative. Enter the argument in parentheses.
Note: The app does not show dx after the derivative. Since the command is in terms of x, the dx is understood. The result 6x - 2 can therefore be written as dy = df = (6x - 2) dx.
More Examples
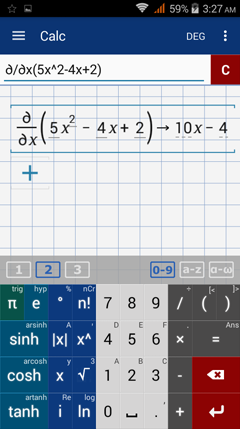
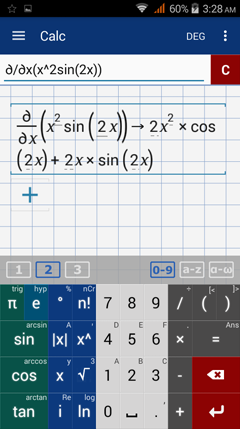
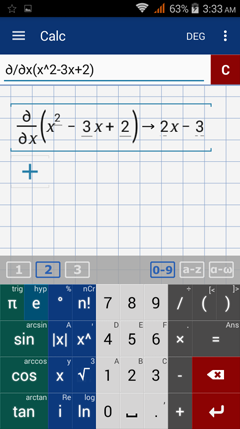
Find the derivative (dy or df) of each function below.
Other Examples