20.1. Gamma Function
The gamma function is an extension of the factorial function except that each gamma argument is shifted by 1. Its formula is defined as the circular permutation of n distinct objects, that is, (n-1)!.
For example, if n = 6, the gamma function of 6 is (6 - 1)! or 5!, which is equal to 120.
To solve for the gamma function of a number, do the following:
To solve for the gamma function of a number, do the following:
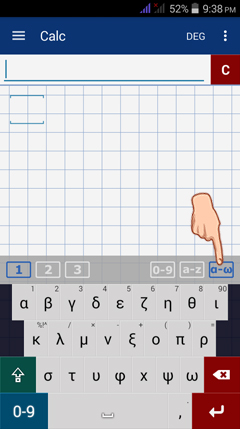
1) Switch to the Greek keyboard by tapping the leftmost keyboard button as shown below.
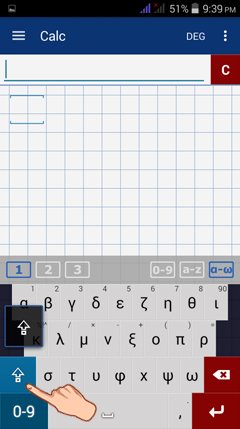
2) Use uppercase Greek letters by tapping the up-arrow on top of the 0-9 key.
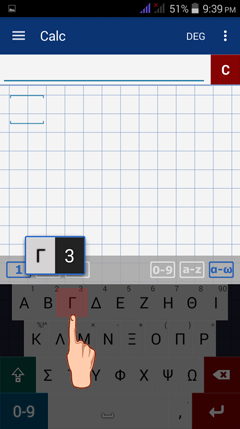
3) Tap Γ (gamma) next to Β (beta).
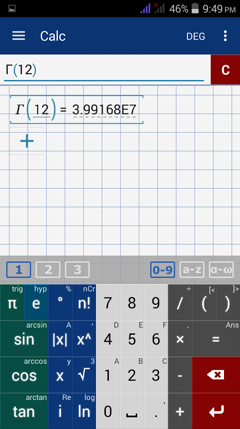
4) Enter the number, or argument, in parentheses.
Examples
Evaluate each gamma function below.
Calculator solutions
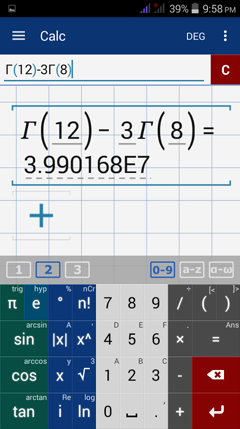
Enter gamma ( Γ ) using the Greek letter keyboard. Type "12" in parentheses.
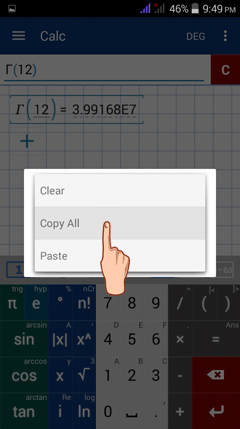
To avoid switching to the Greek keyboard each type to enter gamma, you can use the copy-paste command. After entering the problem for #1, tap and hold the input field to see the copy-paste options.
Tap "Copy All."
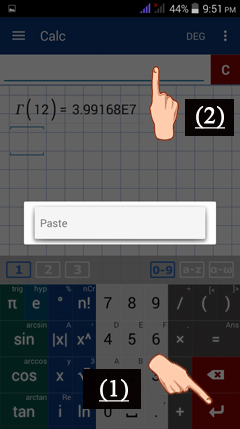
Hit the enter key to go to a new line. Then tap and hold the input field to see the paste option.
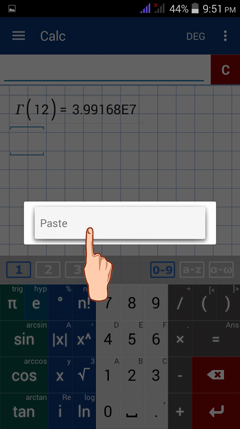
Tap "Paste."
Enter the minus sign, then "3." Tap and hold the input field again to see paste. Tap "Paste."
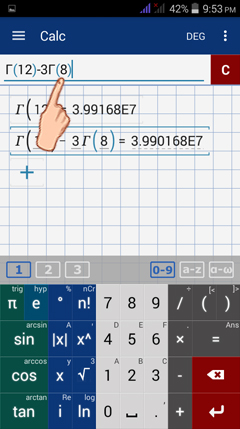
Change the "12" inside the parentheses to "8."
|
Calculator syntax:
|
|
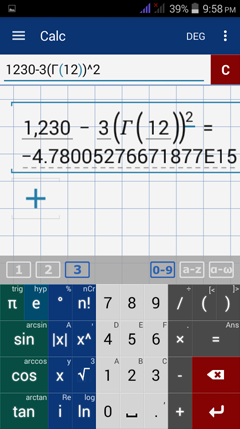
3) You can either paste gamma ( Γ ) using the same procedures or using the Greek keyboard.
|
Calculator syntax:
|
|
4) Enter the function using the syntax shown below.
|
Calculator syntax:
|
|
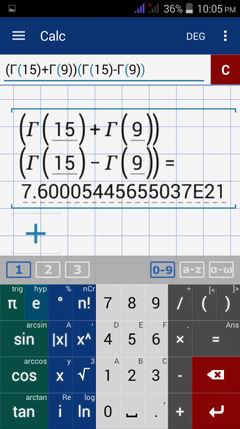
5) Enter the function using the syntax shown below.
|
Calculator syntax:
|
|
