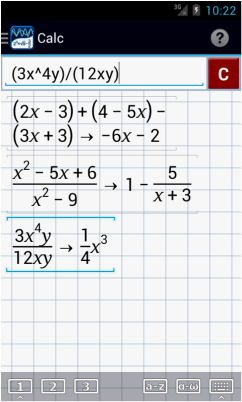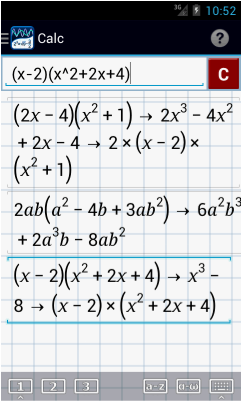7.6. Polynomials
A polynomial is the sum of multiple terms where the terms are raised to different powers of the same variable. Polynomials do not have fractional exponents (e.g. square roots), negative exponents, or variables in the denominator.
To operate on polynomials, enter all arguments as they appear in the problem with one expression per line. Use the x (variable) key to cycle through variables (x, y, z, θ, r), or use the a-z keyboard. Switch back to the 0-9 keyboard to enter operations and exponents.
To operate on polynomials, enter all arguments as they appear in the problem with one expression per line. Use the x (variable) key to cycle through variables (x, y, z, θ, r), or use the a-z keyboard. Switch back to the 0-9 keyboard to enter operations and exponents.
Examples
Perform each indicated operation.
Perform each indicated operation.
1. (2x – 3) + (4 – 5x) – (3x + 3)
| 2. | x2 - 5x + 6 |
| x2 - 9 |
| 3. | 3x4y |
| 12xy |
Calculator solutions
1) Type: (2x-3) + (4-5x) - (3x+3)
2) Type: (x^2 - 5x + 6)/(x^2 - 9)
3) Type: (3x^4y)/(12xy)
1) Type: (2x-3) + (4-5x) - (3x+3)
2) Type: (x^2 - 5x + 6)/(x^2 - 9)
3) Type: (3x^4y)/(12xy)
Polynomial Expansion
Polynomial expansion means expanding a product of sums through distributing rules such as FOIL (first, outside, inner, last).
For example, (x + 2)(x + 3) expands to x^2 + 5x + 6.
= (x + 2)(x + 3)
= x^2 + 3x + 2x + 6 = x^2 + 5x + 6
F O I L
To expand a polynomial, enter all arguments as they appear in the problem and write one expression per line.
Polynomial expansion means expanding a product of sums through distributing rules such as FOIL (first, outside, inner, last).
For example, (x + 2)(x + 3) expands to x^2 + 5x + 6.
= (x + 2)(x + 3)
= x^2 + 3x + 2x + 6 = x^2 + 5x + 6
F O I L
To expand a polynomial, enter all arguments as they appear in the problem and write one expression per line.
Examples
Expand each polynomial.
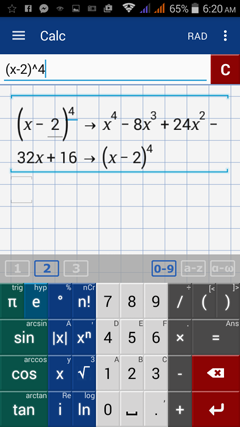
1) (x - 2)^4
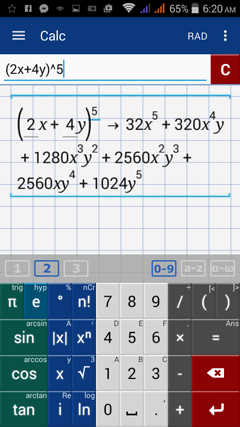
2) (2x + 4y)^5
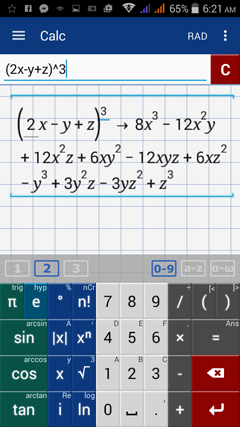
3) (2x - y + z)^3
Calculator solutions
Find variables y and z under the x variable.
1) Type: (x - 2)^4
2) Type: (2x + 4y)^5
3) Type: (2x - y + z)^3
Expand each polynomial.
1) (x - 2)^4
2) (2x + 4y)^5
3) (2x - y + z)^3
Calculator solutions
Find variables y and z under the x variable.
1) Type: (x - 2)^4
2) Type: (2x + 4y)^5
3) Type: (2x - y + z)^3
Multiplying Polynomials: More Examples
Evaluate each of the following.
Evaluate each of the following.
1. (2x – 4)(x2 + 1)
2. 2ab(a2 – 4b + 3ab2)
3. (x – 2)(x2 + 2x + 4)
Calculator solutions
1) Type: (2x-4)(x^2+1)
2) Use the a-z keyboard to type the variables a and b. Type: 2ab(a^2 - 4b + 3ab^2)
3) Type: (x-2)(x^2+2x+4)
1) Type: (2x-4)(x^2+1)
2) Use the a-z keyboard to type the variables a and b. Type: 2ab(a^2 - 4b + 3ab^2)
3) Type: (x-2)(x^2+2x+4)
Factoring Polynomials
Factoring a polynomial means breaking a polynomial into simpler parts (factors).
For example, 2x^2 + 3x - 2 is factored into (2x - 1)(x + 2) because (2x - 1)(x + 2) = 2x^2 + 3x - 2.
So (2x - 1) and (x + 2) are the factors of 2x^2 + 3x - 2.
To factor a polynomial, enter the arguments as they appear in the problem. Enter one expression per line. To see an individual solution, enter one polynomial per workspace.
Note: The app expresses factors in the form: x - c. For example, 2x^2 - 13x + 15 is factored into 2(x - 3/2)(x - 5). To avoid fractions, multiply the coefficient "2" across (x - 3/2) such that 2(x - 3/2)(x - 5) = (2x - 3)(x - 5) = 2x^2 - 13x + 15.
Examples
Factor each polynomial
Factoring a polynomial means breaking a polynomial into simpler parts (factors).
For example, 2x^2 + 3x - 2 is factored into (2x - 1)(x + 2) because (2x - 1)(x + 2) = 2x^2 + 3x - 2.
So (2x - 1) and (x + 2) are the factors of 2x^2 + 3x - 2.
To factor a polynomial, enter the arguments as they appear in the problem. Enter one expression per line. To see an individual solution, enter one polynomial per workspace.
Note: The app expresses factors in the form: x - c. For example, 2x^2 - 13x + 15 is factored into 2(x - 3/2)(x - 5). To avoid fractions, multiply the coefficient "2" across (x - 3/2) such that 2(x - 3/2)(x - 5) = (2x - 3)(x - 5) = 2x^2 - 13x + 15.
Examples
Factor each polynomial
1. x3 – 8
2. x2 + x – 6
3. 2x2 – 13x + 15
Calculator solutions
Enter each expression as it appears in the problem
1) Type: x^3 - 8
2) Type: x^2 + x - 6
3) Type: 2x^2 - 13x + 15
Enter each expression as it appears in the problem
1) Type: x^3 - 8
2) Type: x^2 + x - 6
3) Type: 2x^2 - 13x + 15