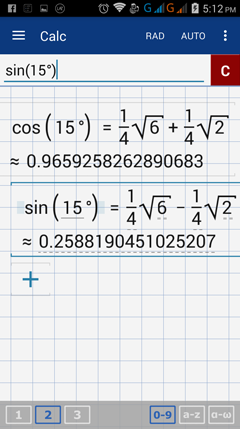13.4. Trigonometric Values of 15° and its Multiples
In the previous section, we discussed how to conveniently find the exact values of the six trigonometric ratios for 30°, 45°, 60°, 90° and their multiples, For other angles such as 15°, 75°, 105°, 165° and other multiples of 15° that are not multiples of 30°, 45°, 60° nor 90°, is a different case. There's no special right triangle that can be used to find the exact trigonometric values of such angles. However, several trigonometric identities can be used to find the exact trigonometric value of an angle.
Consider an angle that measures 15°. As a usual practice in school, to find the exact trigonometric ratios of this angle, we use the difference identify for sine and cosine. Then, apply reciprocal identities or SOHCAHTOA, whichever is more convenient, to solve for the values of the remaining four ratios.
The manual solution for finding the exact cosine and sine value of 15° are shown below.
cos 15° = cos (45° - 30°)
= cos 45° cos 30° + sin 45° sin 30°
= [sqrt(2)/2] [sqrt(3)/2] + [sqrt(2)/2] (1/2)
= sqrt(6)/4 + sqrt(2) / 4
sin 15° = sin (45° - 30°)
= sin 45° cos 30° - cos 45° sin 30°
= [sqrt(2)/2] [sqrt(3)/2] - [sqrt(2)/2] (1/2)
= sqrt(6)/4 - sqrt(2) / 4
Now, let us use the app to calculate the exact value of cosine 15° and sine 15°.
Yes, you've seen it right. This app can also calculate the exact trigonometric ratios of those angles that are multiples of 15° or π /12 but are not multiples of 30°, 45°, 60° nor 90° (π /6, π /4, π /3 nor π /2, respectively).
More Examples
Find the exact value of each trigonometric ratio.
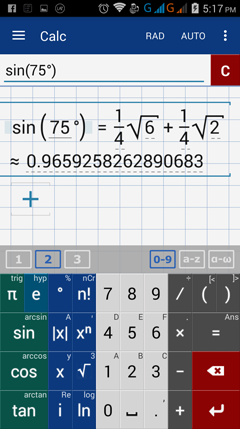
1) sin 75°
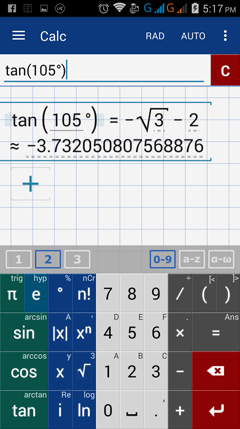
2) tan 105°
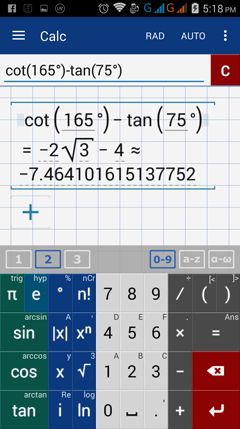
3) cot 165° - tan 75°
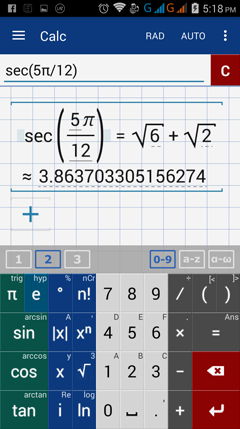
4) sec (5π /12)
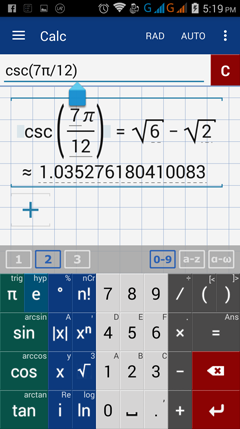
5) csc (7π /12)
Calculator Solutions
Enter each ratio as it appears.
1) Enter: sin (75°)
2) Enter: tan (105°)
3) Enter: cot (165°) - tan(75°)
4) Enter: sec(5π / 12)
5) Enter: csc(7π / 12)