16.2. Second Derivative Key
While the first derivative of a function is the change in y due to a change in x, the second derivative of a function is the change in it's first derivative due to a change in x.
Tap the exponent key (x^) three times to use the second derivative key (x''). Enter the argument in parentheses.
Examples
Find the second derivative of each expression below.
Tap the exponent key (x^) three times to use the second derivative key (x''). Enter the argument in parentheses.
Examples
Find the second derivative of each expression below.
1. 2x3 + 4x2 – 5
2. 2x5 – 3x4 + 2x – 6
Calculator solutions
Enter each expression as given with one per line. Enter the expression in parentheses and tap the exponent key (x^n) three times to enter a second derivative.
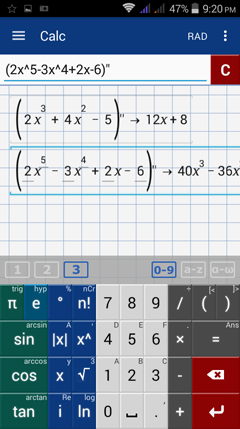
1) Type: (2x^3 + 4x^2 - 5)''
2) Type: (2x^5 - 3x^4 + 2x - 6)''
Enter each expression as given with one per line. Enter the expression in parentheses and tap the exponent key (x^n) three times to enter a second derivative.
1) Type: (2x^3 + 4x^2 - 5)''
2) Type: (2x^5 - 3x^4 + 2x - 6)''