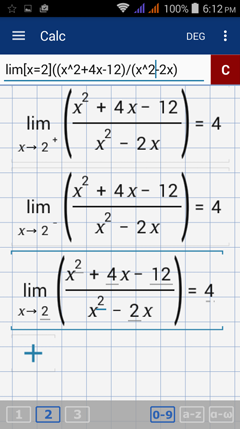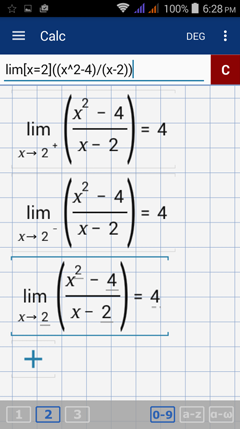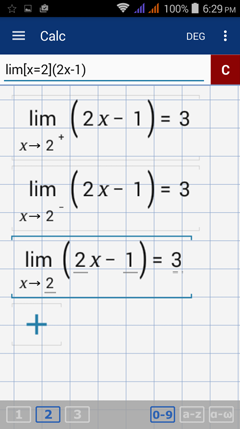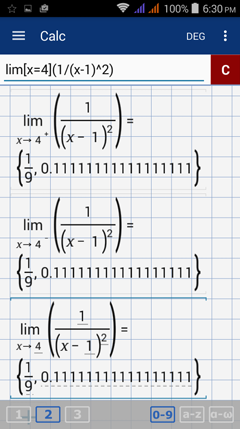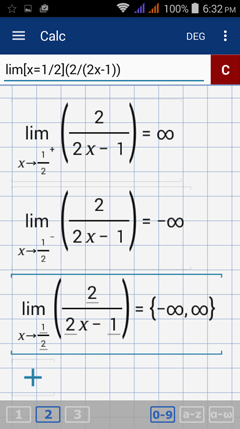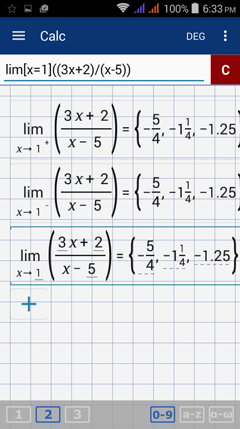15.3. Limit of a Function

The limit of a function f(x) as x approaches c is a real number L.

$\lim_{x\rightarrow c}f(x)=L$

For a limit to exist:
1) The right-hand limit exists.
2) The left-hand limit exists.
3) The right-hand limit is equal to the left-hand limit.

When a limit doesn't exist, several things may be the case:
1) The right-hand limit is not equal to the left-hand limit.
2) The function increases infinitely as x approaches c.
3) The function oscillates between two fixed values as x approaches c.
4) The graph of the function has a jump discontinuity at x = c.
5) The graph of the function has an infinite discontinuity at x = c.

Illustrative Example
Check if the limit exists. If it does, find the limit.

$\lim_{x\rightarrow 2}\frac{x^2+4x-12}{x^2-2x}$

Solution
1) Calculate the left-hand limit.
2) Calculate the right-hand limit.
3) If both limits are equal, then the function has a limit as x approaches c = 2.
The limit is equal to the right-hand limit which is equal to the left-hand limit.

Because the right- and left-hand limits are both equal to 4, the function has a limit of 4 as x approaches 2.

$\lim_{x\rightarrow 2}\frac{x^2+4x-12}{x^2-2x}=4$

More Examples

Check if the limit exists. If it does, find the limit.

$1)\lim_{x\rightarrow 2}\frac{x^2-4}{x-2}$

Calculator solution
Right-hand limit: lim [ x = 2 + ] ( ( x^2 - 4 ) / ( x - 2 ) )
Left-hand limit: lim [ x = 2 - ] ( ( x^2 - 4 ) / ( x - 2 ) )
Limit of the function: lim [ x = 2 ] ( ( x^2 - 4 ) / ( x - 2 ) )

The one-sided limits are equal so the function has a limit of 4 as x approaches 2.

$2)\lim_{x\rightarrow 2}(2x-1)$

Calculator solution
Right-hand limit: lim [ x = 2 + ] ( 2x - 1 )
Left-hand limit: lim [ x = 2 - ] ( 2x - 1 )
Limit of the function: lim [ x = 2 ] ( 2x - 1 )

The one-sided limits are equal so the function has a limit of 3 as x approaches 2.

$3)\lim_{x\rightarrow 4}\frac{1}{(x-1)^2}$

Calculator solution
Right-hand limit: lim [ x = 4 + ] ( 1 / ( x - 1 )^2 )
Left-hand limit: lim [ x = 4 - ] ( 1 / ( x - 1 )^2 )
Limit of the function: lim [ x = 4 ] ( 1 / ( x - 1 )^2 )

The one-sided limits are equal so the limit of the function is 1/9 as x approaches 4.

$4)\lim_{x\rightarrow \frac{1}{2}}\frac{2}{2x-1}$

Calculator solution
Right-hand limit: lim [ x = 1 / 2 + ] ( 2 / ( 2x - 1 ) )
Left-hand limit: lim [ x = 2 - ] ( 2 / ( 2x - 1 ) )
Limit of the function: lim [ x = 2 ] ( 2 / ( 2x - 1 ) )

The one-sided limits are not equal since the right-hand limit is ∞ while the left-hand limit is -∞. So the limit does not exist (DNE).

$5)\lim_{x\rightarrow 1}\frac{3x+2}{x-5}$

Calculator solution
Right-hand limit: lim [ x = 1 + ] ( ( 3x + 2 ) / ( x - 5 ) )
Left-hand limit: lim [ x = 1 - ] ( ( 3x + 2 ) / ( x - 5 ) )
Limit of the function: lim [ x = 1 ] ( ( 3x + 2 ) / ( x - 5 ) )

The one-sided limits are equal so the limit of the function is -5/4 as x approaches 1.

next: 15.4. limit of a polynomial function>

list of contents