6.12. Binary, Octal, Decimal, Hexadecimal Numbers
Numbers can also be represented using the binary, octal and hexadecimal number systems.
Converting Decimal to Binary and Vice Versa
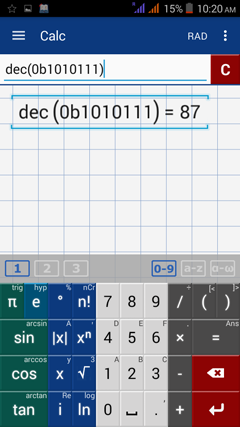
The binary system only uses the digits 0 and 1 to express a number. Each digit "1" in a binary code represents a power of 2 and each "0" represents a zero. For example, the binary code 1010111 means 1(2^6) + 0(2^5) + 1(2^4) + 0(2^3) + 1(2^2) + 1(2^1) + 1(2^0) = 64 + 0 + 16 + 0 + 4 + 2 + 1 = 87, so 1010111 in binary equals the decimal number 87.
In the app, type dec0b1010111 and see that the result is 87. The code “0b” is used to denote the number as a binary number. To convert 87 back to binary, type bin87. The calculator should display 0b1010111. The number following the “0b” code is the binary equivalent of 87.
The binary system only uses the digits 0 and 1 to express a number. Each digit "1" in a binary code represents a power of 2 and each "0" represents a zero. For example, the binary code 1010111 means 1(2^6) + 0(2^5) + 1(2^4) + 0(2^3) + 1(2^2) + 1(2^1) + 1(2^0) = 64 + 0 + 16 + 0 + 4 + 2 + 1 = 87, so 1010111 in binary equals the decimal number 87.
In the app, type dec0b1010111 and see that the result is 87. The code “0b” is used to denote the number as a binary number. To convert 87 back to binary, type bin87. The calculator should display 0b1010111. The number following the “0b” code is the binary equivalent of 87.
Examples
Convert each decimal number to binary.
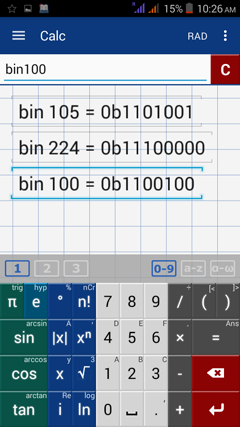
1) 105
2) 224
3) 100
Calculator Solutions
Type "bin" before each number.
1) bin(105)
2) bin(224)
3) bin(100)
Convert each decimal number to binary.
1) 105
2) 224
3) 100
Calculator Solutions
Type "bin" before each number.
1) bin(105)
2) bin(224)
3) bin(100)
Examples
Convert each binary number to a decimal number.
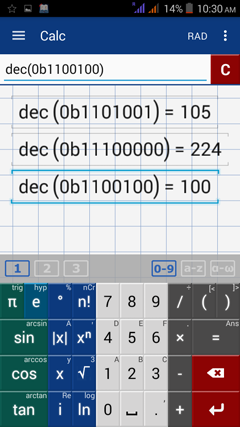
1) 1101001
2) 11100000
3) 1100100
Calculator Solutions
Type "dec" before each argument and denote the binary number by "0b."
1) dec(0b1101001)
2) dec(0b11100000)
3) dec(0b1100100)
Convert each binary number to a decimal number.
1) 1101001
2) 11100000
3) 1100100
Calculator Solutions
Type "dec" before each argument and denote the binary number by "0b."
1) dec(0b1101001)
2) dec(0b11100000)
3) dec(0b1100100)
Converting Decimal to Octal and Vice Versa
The octal number system uses 8 digits (0, 1, 2, 3, 4, 5, 6, and 7) to represent a number. Because the digits only go up to 7, the system replaces the last digit for the number 8 and expresses it as 10, which means 1 × 8^1 + 0(8^0).
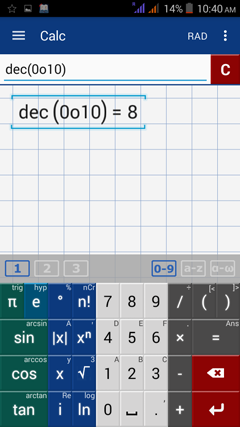
To see this conversion in the app, type oct8 and see that the display shows 0o10, meaning that the decimal number 8 is equivalent to 10 in the octal number system. The code “0o” means that the following number is an octal number.
To convert the octal number 10 back to a decimal number, type dec0o10. The result is 8.
The octal number system uses 8 digits (0, 1, 2, 3, 4, 5, 6, and 7) to represent a number. Because the digits only go up to 7, the system replaces the last digit for the number 8 and expresses it as 10, which means 1 × 8^1 + 0(8^0).
To see this conversion in the app, type oct8 and see that the display shows 0o10, meaning that the decimal number 8 is equivalent to 10 in the octal number system. The code “0o” means that the following number is an octal number.
To convert the octal number 10 back to a decimal number, type dec0o10. The result is 8.
Examples
Convert each decimal number to octal.
1) 105
2) 224
3) 100
Calculator Solutions
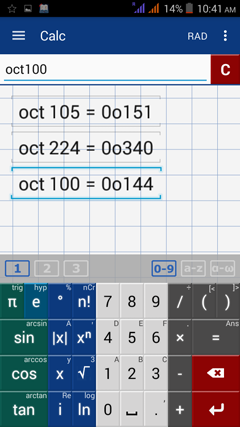
Type "oct" before each argument.
1) oct(105)
2) oct(224)
3) oct(100)
Convert each decimal number to octal.
1) 105
2) 224
3) 100
Calculator Solutions
Type "oct" before each argument.
1) oct(105)
2) oct(224)
3) oct(100)
Examples
Convert each octal number to decimal.
1) 151
2) 340
3) 144
Calculator Solutions
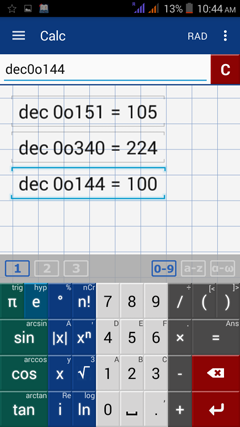
Type "dec" before each argument and denote the octal number by "0o."
1) dec(0o151)
2) dec(0o340)
3) dec(0o144)
Convert each octal number to decimal.
1) 151
2) 340
3) 144
Calculator Solutions
Type "dec" before each argument and denote the octal number by "0o."
1) dec(0o151)
2) dec(0o340)
3) dec(0o144)
Converting Decimal to Hexadecimal and Vice Versa
The hexadecimal number system is a base 16 numeral system. It uses 16 symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F) to represent a number. Unlike the octal and binary systems, it uses the first six letters of the alphabet (A, B, C, D, E and F). This means that after 9, the system counts to A for 10, B for 11, C for 12, D for 13, E for 14, and F for 15. Counting up from 15 replaces the last digit.
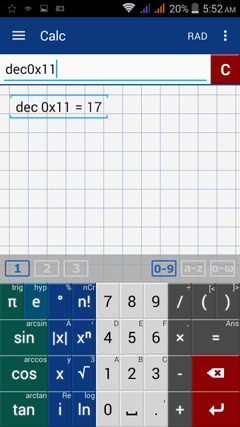
For example, the decimal number 17 is expressed as 11 in the hexadecimal system. To see it in the app, type hex17 and the app will display 0x11. The first two symbols “0x” mean that the following number is a hexadecimal number. To convert the hexadecimal number 11 back to decimal, type dec0x11 and the result will be 17.
The hexadecimal number system is a base 16 numeral system. It uses 16 symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F) to represent a number. Unlike the octal and binary systems, it uses the first six letters of the alphabet (A, B, C, D, E and F). This means that after 9, the system counts to A for 10, B for 11, C for 12, D for 13, E for 14, and F for 15. Counting up from 15 replaces the last digit.
For example, the decimal number 17 is expressed as 11 in the hexadecimal system. To see it in the app, type hex17 and the app will display 0x11. The first two symbols “0x” mean that the following number is a hexadecimal number. To convert the hexadecimal number 11 back to decimal, type dec0x11 and the result will be 17.
Examples
Convert each decimal number to hexadecimal.
1) 105
2) 224
3) 100
Calculator Solutions
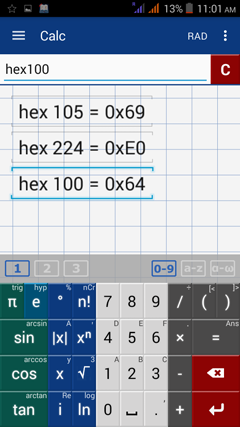
Type "hex" before each argument.
1) hex105
2) hex224
3) hex100
Convert each decimal number to hexadecimal.
1) 105
2) 224
3) 100
Calculator Solutions
Type "hex" before each argument.
1) hex105
2) hex224
3) hex100
Examples
Convert each hexadecimal number to decimal.
1) 69
2) E0
3) 64
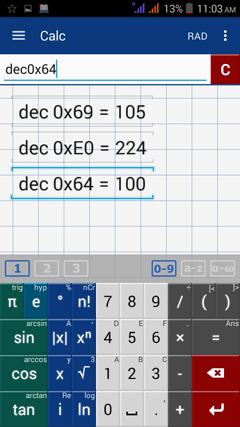
Calculator Solutions
Type "dec" before each argument and denote the hexadecimal by "0x."
1) dec(0x69)
2) dec(0xE0)
3) dec(0x64)
Convert each hexadecimal number to decimal.
1) 69
2) E0
3) 64
Calculator Solutions
Type "dec" before each argument and denote the hexadecimal by "0x."
1) dec(0x69)
2) dec(0xE0)
3) dec(0x64)
Converting Between Number Systems
Remember to enter the code “0b” to convert a binary number, “0o” to convert an octal number, and “0x” to convert a hexadecimal number.
Examples
1) Convert 10011001 to hexadecimal.
2) Convert 1234E to binary.
3) Convert A045 to octal.
4) Convert 012576 to binary.
5) Convert 101011 to octal.
Calculator Solutions
1) Type: hex(0b10011001)
The binary 10011001 is equivalent to 99 in hexadecimal.
2) Type: bin(0x1234E)
The hexadecimal 1234E is equivalent to 10010001101001110.
3) Type: oct0xA045
The hexadecimal A045 is equivalent to 120105 in octal.
4) Type: bin0o012576
The octal 012576 is equivalent to 1010101111110 in binary.
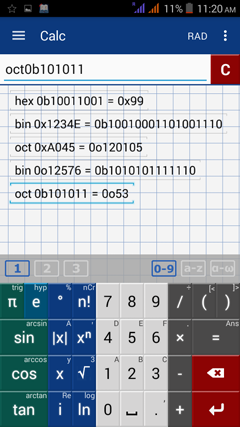
5) Type: oct0b101011
The binary 101011 is equivalent to 53 in octal.
Remember to enter the code “0b” to convert a binary number, “0o” to convert an octal number, and “0x” to convert a hexadecimal number.
Examples
1) Convert 10011001 to hexadecimal.
2) Convert 1234E to binary.
3) Convert A045 to octal.
4) Convert 012576 to binary.
5) Convert 101011 to octal.
Calculator Solutions
1) Type: hex(0b10011001)
The binary 10011001 is equivalent to 99 in hexadecimal.
2) Type: bin(0x1234E)
The hexadecimal 1234E is equivalent to 10010001101001110.
3) Type: oct0xA045
The hexadecimal A045 is equivalent to 120105 in octal.
4) Type: bin0o012576
The octal 012576 is equivalent to 1010101111110 in binary.
5) Type: oct0b101011
The binary 101011 is equivalent to 53 in octal.