16.5. Derivative of Polynomial Functions
Although you can easily find the slope of a linear function by looking at m in y = mx + b, you have to apply derivative rules to find the slope of higher degree polynomials.
To find a derivative, type the expression in parentheses and tap the exponent key (x^) twice.
Examples
For #1-4, find the derivative of each polynomial.
To find a derivative, type the expression in parentheses and tap the exponent key (x^) twice.
Examples
For #1-4, find the derivative of each polynomial.
For #5, find the slope and equation of the tangent line to the curve through the point (3, -4)
Calculator solutions
Type each expression as given. Enter the expression in parentheses and take the derivative by tapping the exponent key (x^n) twice.
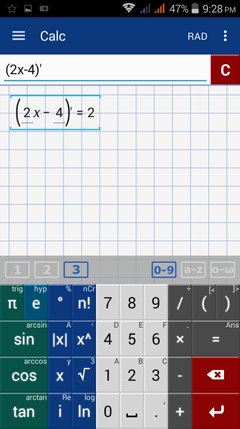
1) Type: (2x - 4)'
Type each expression as given. Enter the expression in parentheses and take the derivative by tapping the exponent key (x^n) twice.
1) Type: (2x - 4)'
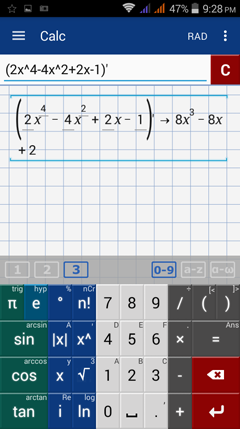
2) Type: (2x^4 - 4x^2 + 2x - 1)'
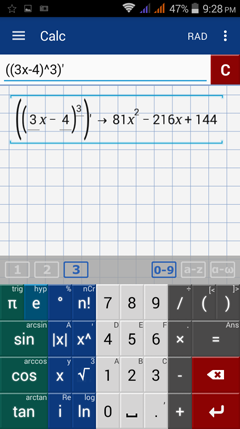
3) Type: ((3x - 4)^3)'
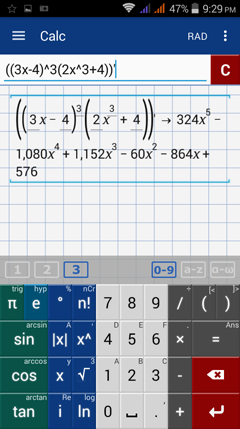
4) Type: ((3x - 4)^3(2x^3 + 4))'
5) In order to find the equation of the tangent line, we need to find the function's derivative and the tangent line's slope at x = 3. Because the app uses the initial value for x to evaluate consequent expressions, we first enter x = 3.
Step 1: Type in the value for x
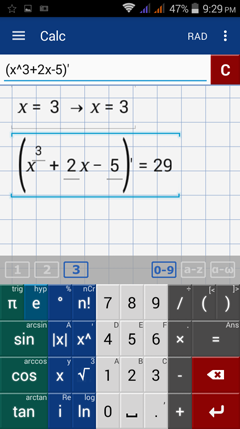
Type the following: x = 3
Step 2: Find the derivative of f(x).
Type the following: (x^3 + 2x - 5)'
The slope shown is the slope of the function at x = 3 which is 29
Step 3: Find the equation of the tangent line.
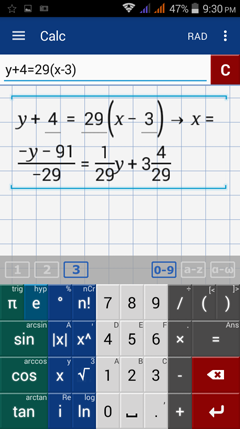
y = mx + b plug (3, -4) and the slope (m = 29) into slope-intercept form
-4 = 29*3 + b
91 = b y- intercept
The equation of the tangent line is y = 29x - 91
Step 1: Type in the value for x
Type the following: x = 3
Step 2: Find the derivative of f(x).
Type the following: (x^3 + 2x - 5)'
The slope shown is the slope of the function at x = 3 which is 29
Step 3: Find the equation of the tangent line.
y = mx + b plug (3, -4) and the slope (m = 29) into slope-intercept form
-4 = 29*3 + b
91 = b y- intercept
The equation of the tangent line is y = 29x - 91