13.2. Trigonometric Function Keys
RAD and DEG Modes
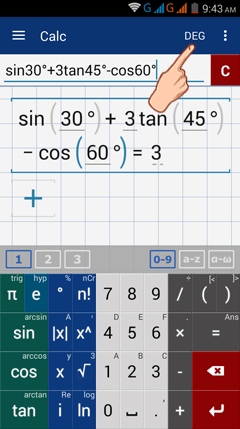
If the trigonometric functions are in degrees, tap RAD to switch the calculator to DEG (degrees mode). All functions will be interpreted in degrees.
To use trigonometric functions in radians, tap DEG to switch back to RAD (radians mode). Functions will be interpreted in radians. To use degrees, add a degree symbol after arguments.
If the trigonometric functions are in degrees, tap RAD to switch the calculator to DEG (degrees mode). All functions will be interpreted in degrees.
To use trigonometric functions in radians, tap DEG to switch back to RAD (radians mode). Functions will be interpreted in radians. To use degrees, add a degree symbol after arguments.
Sine Key
The sine key calculates the sine value of a given angle expressed in radians by default. Tap the º (degree) key to enter an argument in degrees.
Example
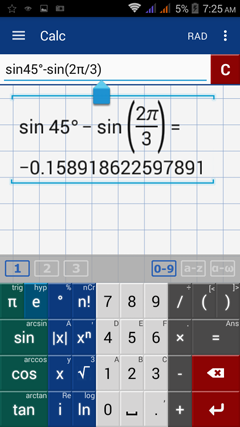
Evaluate sin45º – sin 2π/3
Calculator solution
Note: Make sure to add parentheses around the radian measure 2π/3.
Enter the expression and include the degrees: sin45º – sin (2π/3)
The sine key calculates the sine value of a given angle expressed in radians by default. Tap the º (degree) key to enter an argument in degrees.
Example
Evaluate sin45º – sin 2π/3
Calculator solution
Note: Make sure to add parentheses around the radian measure 2π/3.
Enter the expression and include the degrees: sin45º – sin (2π/3)
Arcsine Key
Tap the sine key twice to use arcsine. It is used to find the measure of an angle given the value of its sine.
Example
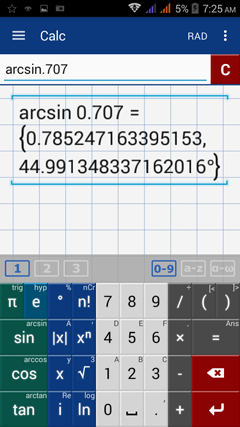
If sin A = 0.707, what is the value of A?
Calculator solution
To solve for A, take the arcsine of 0.707. Double tap the sine key, then type 0.707.
Tap the sine key twice to use arcsine. It is used to find the measure of an angle given the value of its sine.
Example
If sin A = 0.707, what is the value of A?
Calculator solution
To solve for A, take the arcsine of 0.707. Double tap the sine key, then type 0.707.
Cosecant Key
Tap the sine key three times to use the cosecant function.
Example
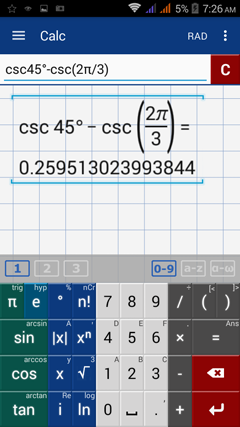
Simplify: csc 45º – csc 2π/3
Calculator solution
Enter the expression and include the degrees: csc 45º – csc (2π/3)
Type cosecant by tapping sin three times.
Tap the sine key three times to use the cosecant function.
Example
Simplify: csc 45º – csc 2π/3
Calculator solution
Enter the expression and include the degrees: csc 45º – csc (2π/3)
Type cosecant by tapping sin three times.
Cosine Key
The cosine key calculates the cosine of a given angle expressed in radians by default. To use degrees, tap the º (degree) key after the argument.
Example
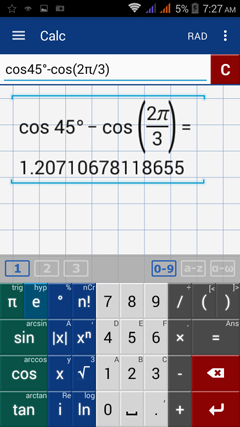
Evaluate: cos45º – cos 2π/3
Calculator solution
Enter the expression and include the degrees: cos45º – cos (2π/3)
The cosine key calculates the cosine of a given angle expressed in radians by default. To use degrees, tap the º (degree) key after the argument.
Example
Evaluate: cos45º – cos 2π/3
Calculator solution
Enter the expression and include the degrees: cos45º – cos (2π/3)
Arccosine Key
Tap the cosine key twice to use arccosine. It is used to find the measure of an angle given its cosine.
Example
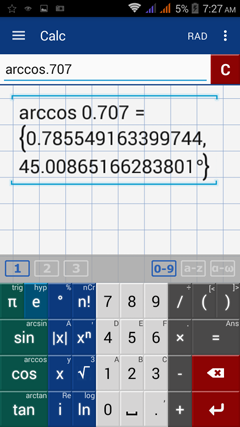
If cos A = 0.707, what is the value of A?
Calculator solution
To solve for A, take the arccosine of 0.707. Tap the cosine key twice, then type 0.707.
Tap the cosine key twice to use arccosine. It is used to find the measure of an angle given its cosine.
Example
If cos A = 0.707, what is the value of A?
Calculator solution
To solve for A, take the arccosine of 0.707. Tap the cosine key twice, then type 0.707.
Secant Key
Tap the sine key three times to use secant.
Example
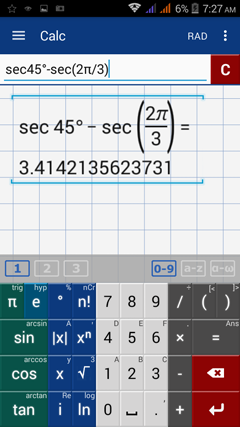
Simplify: sec 45º – sec 2π/3
Calculator solution
Enter the expression and include the degrees: sec 45º – sec (2π/3)
Type secant by tapping cos three times.
Tap the sine key three times to use secant.
Example
Simplify: sec 45º – sec 2π/3
Calculator solution
Enter the expression and include the degrees: sec 45º – sec (2π/3)
Type secant by tapping cos three times.
Tangent Key
The tangent key calculates the tangent of a given angle in radians by default. Tap the º (degree) key to use degrees.
Example
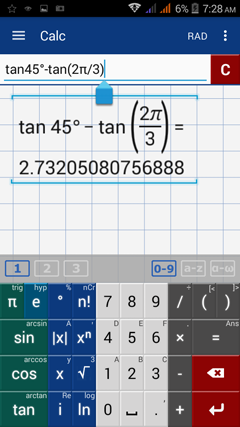
tan 45º – tan 2π/3
Calculator solution
Enter the expression and include the degrees: tan 45º – tan (2π/3)
The tangent key calculates the tangent of a given angle in radians by default. Tap the º (degree) key to use degrees.
Example
tan 45º – tan 2π/3
Calculator solution
Enter the expression and include the degrees: tan 45º – tan (2π/3)
Arctangent Key
Tap the tangent key twice to use arctangent. It is used to find the measure of an angle given the value of its tangent.
Example
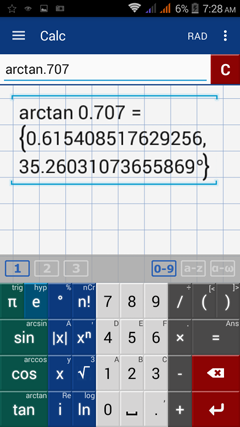
If tan A = 0.707, what is the value of A?
Calculator solution
To solve, find the arctangent of 0.707. Tap the tan key twice, then type 0.707.
Tap the tangent key twice to use arctangent. It is used to find the measure of an angle given the value of its tangent.
Example
If tan A = 0.707, what is the value of A?
Calculator solution
To solve, find the arctangent of 0.707. Tap the tan key twice, then type 0.707.
Cotangent Key
Tap the tan key three times to find the cotangent.
Example
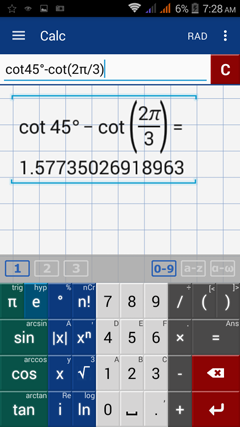
Simplify: cot 45º – cot 2π/3
Calculator solution
Enter the expression and include the degrees: cot 45º – cot (2π/3)
Type cotangentby tapping tan three times.
Tap the tan key three times to find the cotangent.
Example
Simplify: cot 45º – cot 2π/3
Calculator solution
Enter the expression and include the degrees: cot 45º – cot (2π/3)
Type cotangentby tapping tan three times.