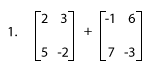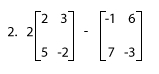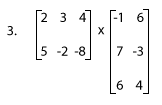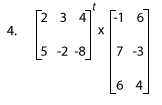12.1 Matrix Operations
Enter each matrix using brackets. Select open brackets by tapping the open parentheses key twice and select closed brackets by tapping the closed parentheses key twice. Separate data entries using a space and rows of elements using another set of brackets.
Addition and Subtraction
Matrices must have the same corresponding number of rows and columns for addition and subtraction. Missing elements will be replaced with zeros.
Examples
Matrices must have the same corresponding number of rows and columns for addition and subtraction. Missing elements will be replaced with zeros.
Examples
Calculator solution
Note: tap ( or ) twice to use brackets [ or ].
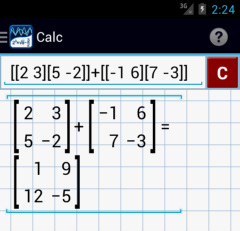
1) Enter: [[2 3][5 -2]] + [[-1 6][7 -3]]
Note: tap ( or ) twice to use brackets [ or ].
1) Enter: [[2 3][5 -2]] + [[-1 6][7 -3]]
Calculator solution
Note: tap ( or ) twice to use brackets [ or ].
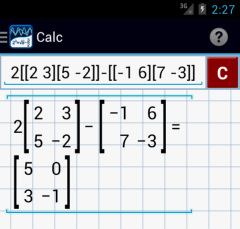
2) Enter: 2[[2 3][5 -2]] - [[-1 6][7 -3]]
Note: tap ( or ) twice to use brackets [ or ].
2) Enter: 2[[2 3][5 -2]] - [[-1 6][7 -3]]
Multiplication
Note that if you want to multiply two matrices with dimensions k (rows) by l (columns) and m (rows) by n (columns), the resulting matrix will always have dimensions k (rows) by n (columns). If l > m, extra rows or columns will be ignored because the number of columns in the first matrix must equal the number of rows in the second.
Examples
Note that if you want to multiply two matrices with dimensions k (rows) by l (columns) and m (rows) by n (columns), the resulting matrix will always have dimensions k (rows) by n (columns). If l > m, extra rows or columns will be ignored because the number of columns in the first matrix must equal the number of rows in the second.
Examples
Calculator solution
Note: tap ( or ) twice to use brackets [ or ].
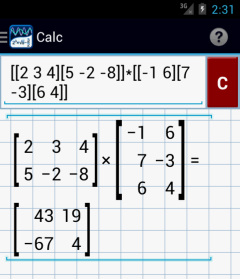
3) Enter: [[2 3 4][5 -2 -8]] × [[-1 6][7 -3][6 4]]
Note: tap ( or ) twice to use brackets [ or ].
3) Enter: [[2 3 4][5 -2 -8]] × [[-1 6][7 -3][6 4]]
Calculator solution
Note: tap ( or ) twice to use brackets [ or ].
Enter ^T by tapping the absolute value key |x| six times or by selecting it from the function's drop-down menu.
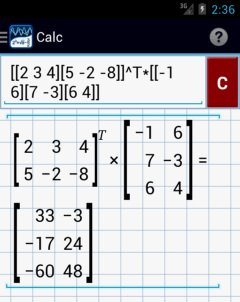
4) Enter: [[2 3 4][5 -2 -8]]^T × [[-1 6][7 -3][6 4]]
Note: tap ( or ) twice to use brackets [ or ].
Enter ^T by tapping the absolute value key |x| six times or by selecting it from the function's drop-down menu.
4) Enter: [[2 3 4][5 -2 -8]]^T × [[-1 6][7 -3][6 4]]
Matrix Powers
Matrices can be raised to positive integer powers. The result is the same as multiplying the matrix by itself (n-1) times.
Inverse Matrices
To find the inverse matrix, raise the original matrix to a power of -1. You can only do this with square matrices that have a non-zero determinant. Note that division between two matrices is defined as multiplying the numerator by the inverse matrix of the denominator, e.g. A/B = A*(B^-1).
Example
Matrices can be raised to positive integer powers. The result is the same as multiplying the matrix by itself (n-1) times.
Inverse Matrices
To find the inverse matrix, raise the original matrix to a power of -1. You can only do this with square matrices that have a non-zero determinant. Note that division between two matrices is defined as multiplying the numerator by the inverse matrix of the denominator, e.g. A/B = A*(B^-1).
Example
Calculator solution
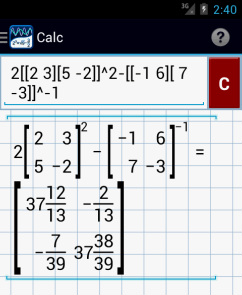
Note: tap ( or ) twice to use brackets [ or ].
Use the exponent key x^n to enter the exponents.
5) Enter: 2[[2 3][5 -2]]^2 - [[-1 6][7 -3]]^-1
Note: tap ( or ) twice to use brackets [ or ].
Use the exponent key x^n to enter the exponents.
5) Enter: 2[[2 3][5 -2]]^2 - [[-1 6][7 -3]]^-1
Vector Cross and Dot Product
To find a vector cross product, the vectors must have three elements. Vectors with fewer than three elements will be extended with zeros. Use the × multiplication sign to find the cross product between two vectors.
To find a dot or scalar product, use the dot multiplication sign by tapping the multiplication sign twice. The dot also works when multiplying scalars.
Examples
1. Find the cross product of [1, 2, 3] and [4, 5, 6]
2. Find the dot product of [1, 2, 3] and [4, 5, 6]
Calculator solutions
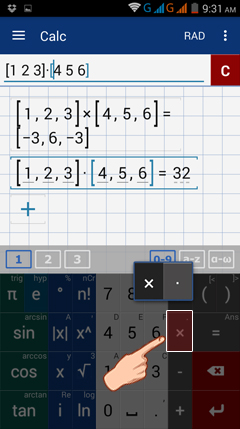
Note: tap ( or ) twice to use brackets [ or ].
1) Enter: [1 2 3] × [4 5 6]
2) Enter: [1 2 3] ∙ [4 5 6]. Enter the dot product by tapping the multiplication key ( × ) twice.
To find a vector cross product, the vectors must have three elements. Vectors with fewer than three elements will be extended with zeros. Use the × multiplication sign to find the cross product between two vectors.
To find a dot or scalar product, use the dot multiplication sign by tapping the multiplication sign twice. The dot also works when multiplying scalars.
Examples
1. Find the cross product of [1, 2, 3] and [4, 5, 6]
2. Find the dot product of [1, 2, 3] and [4, 5, 6]
Calculator solutions
Note: tap ( or ) twice to use brackets [ or ].
1) Enter: [1 2 3] × [4 5 6]
2) Enter: [1 2 3] ∙ [4 5 6]. Enter the dot product by tapping the multiplication key ( × ) twice.