15.6. Limit of a Radical Function
The limit of a radical function can be found by taking a radical function of the limit using the following definition:
Illustrative Example
Calculate the limit of the square root of (2x + 3) as x approaches 3.
Solution
1) Find the limit of (2x + 3) as x approaches 3.
f(3) = (2*3 + 3) = 9
2) Take the square root of 9 to get 3.
3) The limit of the square root of (2x + 3) as x approaches 3 is 3
Solution
1) Find the limit of (2x + 3) as x approaches 3.
f(3) = (2*3 + 3) = 9
2) Take the square root of 9 to get 3.
3) The limit of the square root of (2x + 3) as x approaches 3 is 3
More examples
Evaluate the limit of each radical function below if it exists.
Evaluate the limit of each radical function below if it exists.
Calculator solution
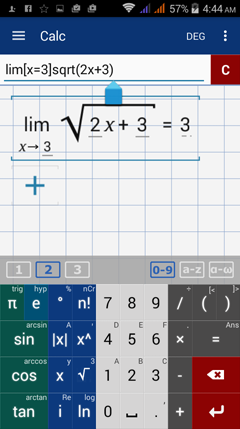
Type in: lim [ x = 3 ] - sqrt( 2x + 3 )
Type in: lim [ x = 3 ] - sqrt( 2x + 3 )
Calculator solution
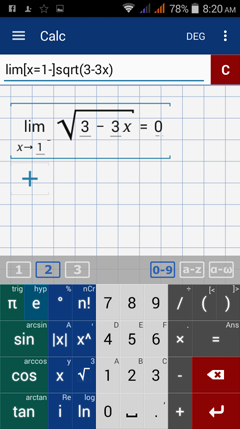
Type in: lim [ x = 1- ] sqrt( 3 - 3x )
Type in: lim [ x = 1- ] sqrt( 3 - 3x )
Calculator solution
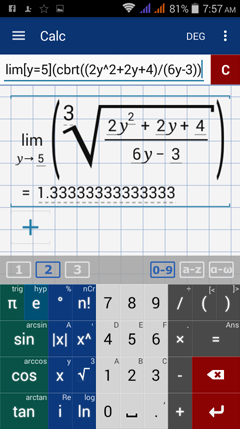
Type in: lim [ y = 5 ] ( cbrt( ( 2y^2 + 2y + 4 ) / ( 6y - 3 ) )
Type in: lim [ y = 5 ] ( cbrt( ( 2y^2 + 2y + 4 ) / ( 6y - 3 ) )
Calculator solution
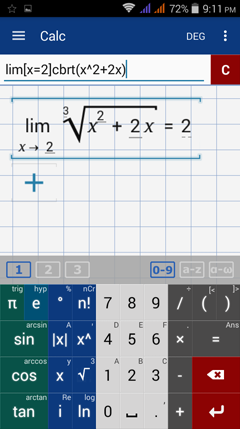
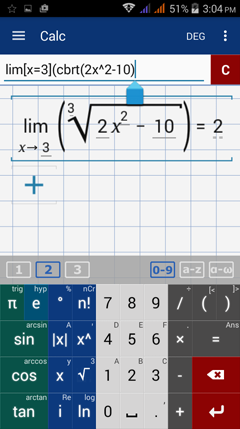
Type in: lim [ x = 3 ] ( cbrt( 2x^2 - 10 ) )
Type in: lim [ x = 3 ] ( cbrt( 2x^2 - 10 ) )
Other Examples
Limit in a Restricted Domain
Similar to a rational function, the limit of a radical function may not exist. To check whether it exists, find the left- and right-hand limits. If the one-sided limits are equal, the limit exists.
Illustrative Example
Evaluate the limit.
Illustrative Example
Evaluate the limit.
Solution
Find the left- and right-hand limits by choosing numbers from the left and right that approach x = 4.
x 3.9 3.99 3.999 3.9999 4 4.0001 4.001 4.01 4.1
y -0.623 -0.625 -0.625 -0.625 undefined -0.625 -0.625 -0.625 -0.627
As x approaches 4 from the left and right, the function approaches -0.625, so the limit of the rational expression is -0.625.
Calculator solution
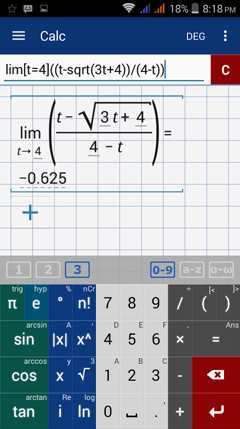
Type in: lim [ t = 4 ] ( ( t - sqrt( 3t + 4 ) ) / ( 4 - t ) )
Find the left- and right-hand limits by choosing numbers from the left and right that approach x = 4.
x 3.9 3.99 3.999 3.9999 4 4.0001 4.001 4.01 4.1
y -0.623 -0.625 -0.625 -0.625 undefined -0.625 -0.625 -0.625 -0.627
As x approaches 4 from the left and right, the function approaches -0.625, so the limit of the rational expression is -0.625.
Calculator solution
Type in: lim [ t = 4 ] ( ( t - sqrt( 3t + 4 ) ) / ( 4 - t ) )
More Examples
Evaluate each limit if it exists.
Evaluate each limit if it exists.
Calculator solution
Type in: lim [ h = 0 ] ( ( sqrt( 1 + h ) - 1 ) / h )
Type in: lim [ h = 0 ] ( ( sqrt( 1 + h ) - 1 ) / h )
Calculator solution
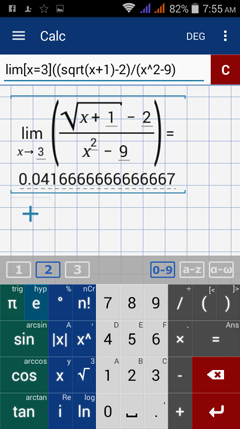
Type in: lim [ x = 3 ] ( ( sqrt( x + 1 ) - 2 ) / ( x^2 - 9 ) )
Type in: lim [ x = 3 ] ( ( sqrt( x + 1 ) - 2 ) / ( x^2 - 9 ) )
The Limit Does Not Exist
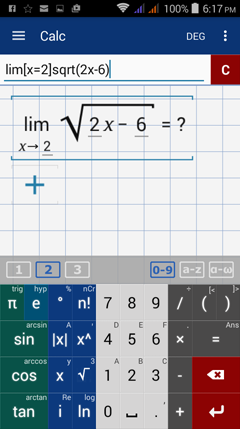
The limit of a radical function does not exist when c is not in the domain of the function. For example, the domain of sqrt( 2x - 6) is the set of real numbers greater than or equal to 3. If x is less than 3, the range of the function belongs in the set of imaginary numbers. Because the values of the function are not in the set of real numbers, the limit does not exist.
Note: trying to find the limit of a radical function as x approaches a number outside the real domain of the function will show a "?" as the result. This means that the limit does not exist.
Note: trying to find the limit of a radical function as x approaches a number outside the real domain of the function will show a "?" as the result. This means that the limit does not exist.
More Examples
Evaluate the limit of each radical function if it exists.
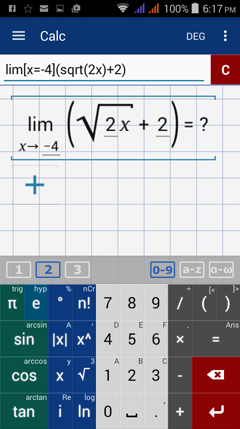
Calculator solution
Type in: lim [ x = -4 ] ( sqrt( 2x ) + 2 )
Since -4 is not in the domain of sqrt( 2x ) + 2, the limit does not exist.
Type in: lim [ x = -4 ] ( sqrt( 2x ) + 2 )
Since -4 is not in the domain of sqrt( 2x ) + 2, the limit does not exist.
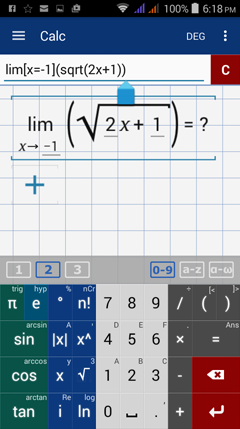
Calculator solution
Type in: lim [ x = -1 ] ( sqrt( 2x + 1 ) )
Since -1 is not in the domain of sqrt( 2x + 1 ), the limit does not exist.
Type in: lim [ x = -1 ] ( sqrt( 2x + 1 ) )
Since -1 is not in the domain of sqrt( 2x + 1 ), the limit does not exist.