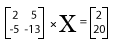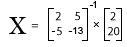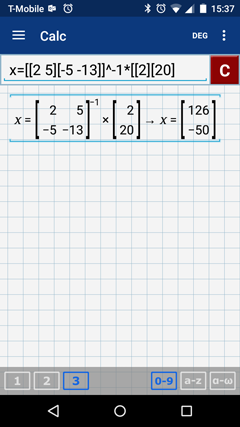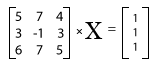12.6. Solving Systems of Linear Equations using Matrix Equations
Matrix Multiplication
If AX = B, then X = A^(-1)*B. A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.
To solve for the variable matrix, divide the constant matrix by the coefficient matrix. To divide B (constant matrix) by A (coefficient matrix), multiply both sides of the equation by the inverse of matrix A.
Enter each matrix using brackets and find the inverse of the coefficient matrix by raising it to a power of -1 using the exponent key. Separate elements using a space and rows using additional brackets.
If AX = B, then X = A^(-1)*B. A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.
To solve for the variable matrix, divide the constant matrix by the coefficient matrix. To divide B (constant matrix) by A (coefficient matrix), multiply both sides of the equation by the inverse of matrix A.
Enter each matrix using brackets and find the inverse of the coefficient matrix by raising it to a power of -1 using the exponent key. Separate elements using a space and rows using additional brackets.
Example 1
Solve a system of equations by converting it into a matrix equation and using the inverse of the coefficient matrix.
Calculator solution
Step 1: Transform the system into a matrix equation.
Solve a system of equations by converting it into a matrix equation and using the inverse of the coefficient matrix.
Calculator solution
Step 1: Transform the system into a matrix equation.
Step 2: Solve for X.
Note: tap ( or ) twice to use brackets [ or ].
Step 3: Enter the following: x = [[2 5][-5 -13]]^-1 * [[2] [20]]
The solution set is (126, -50).
Step 3: Enter the following: x = [[2 5][-5 -13]]^-1 * [[2] [20]]
The solution set is (126, -50).
Example 2
Solve a system of equations by converting it into a matrix equation and using the inverse of the coefficient matrix.
Calculator solution
Step 1: Transform the system into a matrix equation.
Solve a system of equations by converting it into a matrix equation and using the inverse of the coefficient matrix.
Calculator solution
Step 1: Transform the system into a matrix equation.
Step 2: Solve for X.
Note: double tap ( or ) for corresponding brackets [ or ].
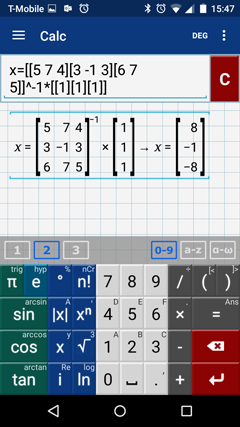
Step 3: Enter the following: x = [[5 7 4][3 -1 3][6 7 5]]^-1 * [[1] [1] [1]]
The solution set is the ordered triple (8, -1, -8).
Step 3: Enter the following: x = [[5 7 4][3 -1 3][6 7 5]]^-1 * [[1] [1] [1]]
The solution set is the ordered triple (8, -1, -8).