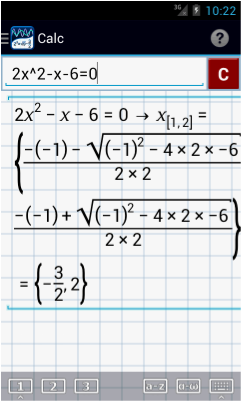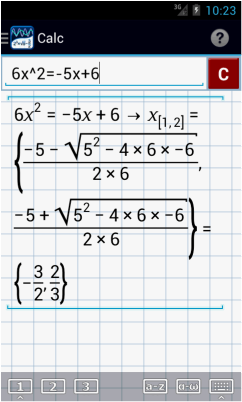8.3. Quadratic Equations
A quadratic equation is a second degree polynomial. It can be written in the form:
The roots are the solutions that make the quadratic equation true. When a quadratic equation is written in the form ax^2 + bx + c, solving the equation means finding a value of x that makes the equation equal to zero. Because a quadratic equation is a 2nd degree polynomial, it can have up to 2 roots.
Quadratic equations can be solved through factoring, the quadratic formula, or approximation. The app solves quadratic equations through the general quadratic formula, the most accurate method.
Examples
Find the roots of each equation below.
Quadratic equations can be solved through factoring, the quadratic formula, or approximation. The app solves quadratic equations through the general quadratic formula, the most accurate method.
Examples
Find the roots of each equation below.
1. 2x2 – x – 6 = 0
2. 6x2 = -5x + 6
Calculator solutions
1) Enter the equation as it appears in the problem: 2x^2 - x - 6 = 0. The solution set is (-3/2, 2).
1) Enter the equation as it appears in the problem: 2x^2 - x - 6 = 0. The solution set is (-3/2, 2).
Solution by hand
Factor 2x^2 - x - 6 into (2x + 3)(x - 2) and set it equal to 0.
In order to solve the equation, either (2x + 3) or (x - 2) must be equal to 0
(2x + 3) = 0 x = -3/2
(x - 2) = 0 x = 2
The two roots are x = 2 and x = -3/2.
2) Enter the equation: 6x^2 = 5x + 6. The solution set is (-3/2, 2/3).
Factor 2x^2 - x - 6 into (2x + 3)(x - 2) and set it equal to 0.
In order to solve the equation, either (2x + 3) or (x - 2) must be equal to 0
(2x + 3) = 0 x = -3/2
(x - 2) = 0 x = 2
The two roots are x = 2 and x = -3/2.
2) Enter the equation: 6x^2 = 5x + 6. The solution set is (-3/2, 2/3).
Graphing Solutions
1) Find the roots of the following:
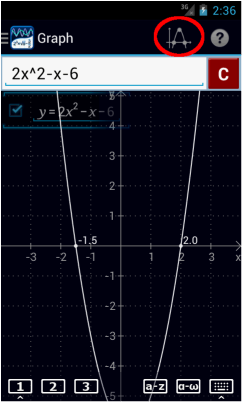
2x2 – x – 6 = 0
Calculator solutions
Enter the expression: 2x^2 - x - 6
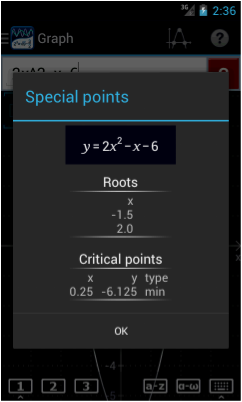
Tap the special points icon in the top right to display the roots and critical points of the graph. The roots of an equation are the points where the graph intersects the x-axis.
Enter the expression: 2x^2 - x - 6
Tap the special points icon in the top right to display the roots and critical points of the graph. The roots of an equation are the points where the graph intersects the x-axis.
2) Find the roots of:
6x2 = -5x + 6
Calculator solution
Enter the equation by rearranging it as "y =" i.e. y = ax^2 + bx + c. The equation becomes y = 6x^2 + 5x - 6.
Tap the special points icon in the top right to display the roots and critical points of the graph. The roots of an equation are the points where the graph intersects the x-axis.
Enter the equation by rearranging it as "y =" i.e. y = ax^2 + bx + c. The equation becomes y = 6x^2 + 5x - 6.
Tap the special points icon in the top right to display the roots and critical points of the graph. The roots of an equation are the points where the graph intersects the x-axis.