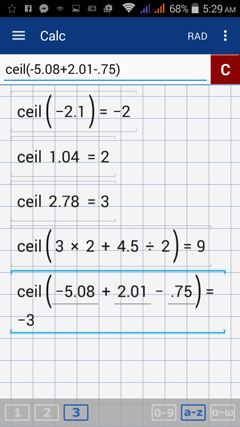6.7.3. Least Integer is the Ceiling Function
The ceiling function (also called the least integer function) maps a real number onto the next highest integer. In general, ceiling(x) is the smallest integer not less than x.
To find the ceiling of a real number x, type the word “ceil” using the letter keys. Then enter the number. If the argument is longer than one term, enclose it in parentheses.
To find the ceiling of a real number x, type the word “ceil” using the letter keys. Then enter the number. If the argument is longer than one term, enclose it in parentheses.
Examples
For each number below, find the ceiling value.
1) -2.1
2) 1.04
3) 2.78
4) 3 × 2 + 4.5 ÷ 2
5) (-5.08 + 2.01 – 0.75)
Calculator solutions
Type "ceil" before each argument.
1) ceil(-2.1)
2) ceil1.04
3) ceil2.78
4) ceil(3 × 2 + 4.5 ÷ 2)
5) ceil(-5.08 + 2.01 – 0.75)
For each number below, find the ceiling value.
1) -2.1
2) 1.04
3) 2.78
4) 3 × 2 + 4.5 ÷ 2
5) (-5.08 + 2.01 – 0.75)
Calculator solutions
Type "ceil" before each argument.
1) ceil(-2.1)
2) ceil1.04
3) ceil2.78
4) ceil(3 × 2 + 4.5 ÷ 2)
5) ceil(-5.08 + 2.01 – 0.75)