11.8. Rational Functions
A rational function can be written in the form f(x) = p(x)/q(x) where p(x) and q(x) are polynomial functions. It can be defined at all values of x except when q(x) = 0 where the the graph either has a hole or an asymptote.
To graph a rational function:
1) If the equation is defined explicitly i.e. "y =," enter only the rational expression with the numerator and denominator in parentheses and use the fraction key ( / ) to separate them.
2) If the equation is defined implicitly, enter the entire equation as given.
3) To sketch graphs on the same coordinate axes, enter one equation per line.
Examples
Sketch the graphs of the following rational functions.
To graph a rational function:
1) If the equation is defined explicitly i.e. "y =," enter only the rational expression with the numerator and denominator in parentheses and use the fraction key ( / ) to separate them.
2) If the equation is defined implicitly, enter the entire equation as given.
3) To sketch graphs on the same coordinate axes, enter one equation per line.
Examples
Sketch the graphs of the following rational functions.
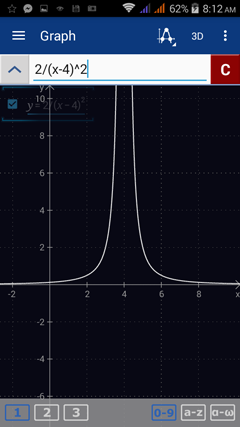
| 1 . y = | 2 |
| (x-4)2 |
| 2 . y = | x+2 |
| 2x-6 |
Calculator solutions
1) Enter the expression: 2/(x -4)^2. Hit enter.
2) Enter the expression: (x + 2)/(2x - 6).
Check the box next to each function to display the discontinuities.
1) Enter the expression: 2/(x -4)^2. Hit enter.
2) Enter the expression: (x + 2)/(2x - 6).
Check the box next to each function to display the discontinuities.
To look the graphs separately, enter each equation on a separate workspace.