19.6.4. Variance and Standard Deviation
Variance and standard deviation are the most common measures of spread in statistical hypothesis tests. Variance refers to the average of the squared differences between each data value and the mean, and standard deviation is the square root of the variance. Variance is expressed in squared units while standard deviation is expressed in the same units as the data values.
Calculating the Variance and Standard Deviation of Ungrouped Data Sets
To find the variance and standard deviation:
1) Find the mean of the data set.
2) Subtract the mean from each data value.
3) Take the square of each difference.
4) Find the average of the squared differences, but divide by (n - 1) if the data came from a sample. Divide by n if the data set is the population. The average is the value of the variance.
5) Take the square root of the variance to get the standard deviation.
Illustrative Example
Find the variance and standard deviation of the data set.
12, 5, 6, 8, 9
Solution
1) Find the average of the data values.
average = (12 + 5 + 6 + 8 + 9)/5 = 8
2) Subtract the mean from each data value.
X X - Mean
12 4
5 -3
6 -2
8 0
9 1
3) Square each difference.
X X - Mean (X - Mean)^2
12 4 16
5 -3 9
6 -2 4
8 0 0
9 1 1
4) Find the average of the squared differences.
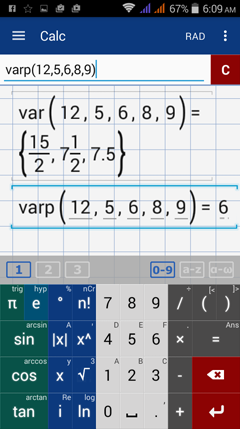
Population variance = (16 + 9 + 4 + 0 + 1)/5 = 6
Sample variance = (16 + 9 + 4 + 0 + 1)/ (5 - 1) = 7.5
5) Take the square root of the variance to find the standard deviation.
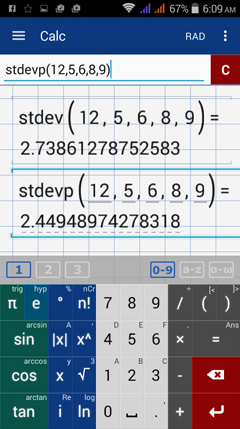
Population standard deviation = square root (6) = 2.4494897
Sample standard deviation = square root (7.5) = 2.738612787
The manual calculations of the variance and standard deviation are simple for small data sets, but it is easier to use the app for data sets that are large. The values for the variance and standard deviation can be found by using var and stdev for sample data or varp and setdevp for population data respectively.
Calculating the Variance and Standard Deviation of Ungrouped Data Sets
To find the variance and standard deviation:
1) Find the mean of the data set.
2) Subtract the mean from each data value.
3) Take the square of each difference.
4) Find the average of the squared differences, but divide by (n - 1) if the data came from a sample. Divide by n if the data set is the population. The average is the value of the variance.
5) Take the square root of the variance to get the standard deviation.
Illustrative Example
Find the variance and standard deviation of the data set.
12, 5, 6, 8, 9
Solution
1) Find the average of the data values.
average = (12 + 5 + 6 + 8 + 9)/5 = 8
2) Subtract the mean from each data value.
X X - Mean
12 4
5 -3
6 -2
8 0
9 1
3) Square each difference.
X X - Mean (X - Mean)^2
12 4 16
5 -3 9
6 -2 4
8 0 0
9 1 1
4) Find the average of the squared differences.
Population variance = (16 + 9 + 4 + 0 + 1)/5 = 6
Sample variance = (16 + 9 + 4 + 0 + 1)/ (5 - 1) = 7.5
5) Take the square root of the variance to find the standard deviation.
Population standard deviation = square root (6) = 2.4494897
Sample standard deviation = square root (7.5) = 2.738612787
The manual calculations of the variance and standard deviation are simple for small data sets, but it is easier to use the app for data sets that are large. The values for the variance and standard deviation can be found by using var and stdev for sample data or varp and setdevp for population data respectively.
Examples
Calculate the variance and standard deviation of each data set below.
1) The heights (in inches) of all 30 employees at a manufacturing company are listed below.
72, 56, 75, 95, 105, 67, 78, 89, 95, 100, 88, 98, 75, 120, 98, 97, 89, 85, 90, 95, 89, 69, 90, 56, 87, 112, 125, 87, 99, 100
2) The ages in years of 15 randomly selected students at a college are as follows:
16, 18, 20, 21, 22, 17, 19, 15, 16, 20, 16, 18, 21, 20, 19
Calculator solutions
1) Since the data set contains the heights for all 30 employees, the data set represents a population so we use varp for variance and stdevp for standard deviation.
a) Calculating the population variance
Enter the data set as a matrix. Use brackets and separate data values with a comma.
E.g. A = [72, 56, 75, 95, 105, 67, 78, 89, 95, 100, 88, 98, 75, 120, 98, 97, 89, 85, 90, 95, 89, 69, 90, 56, 87, 112, 125, 87, 99, 100]
Note: To check if you entered all of the data values, you can find the length of the data set by entering length(A). Select "length" by holding the factorial (n!) key.
Hold the factorial (n!) key and select varp. Type the name of the matrix, A.
E.g. varp(A)
b) Calculating the population standard deviation.
Since the data set has already been entered as a matrix, you can refer to it by its matrix name, A in this case.
To calculate the standard deviation, hold the factorial (n!) key and select stdevp. Enter the matrix in parentheses.
E.g. stdevp(A)
2) Since the data set is composed of the ages of a select number of students at the college, it represents a sample of values. In this case, we use the commands var for variance and stdev for standard deviation.
a) Calculating the sample variance
Enter the data set as a matrix. Use brackets and separate data values with a comma.
E.g. B = [16, 18, 20, 21, 22, 17, 19, 15, 16, 20, 16, 18, 21, 20, 19]
Note: To check if you entered all of the data values, you can find the length of the data set by entering length(A). Select "length" by holding the factorial (n!) key.
Hold the factorial (n!) key and select var. Type the name of the matrix, B.
E.g. var(B)
b) Calculating the sample standard deviation.
Since the data set has already been entered as a matrix, you can refer to it by its matrix name, B in this case.
To calculate the standard deviation, hold the factorial (n!) key and select stdev. Enter the matrix in parentheses.
E.g. stdev(B)