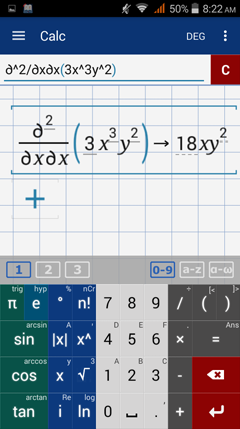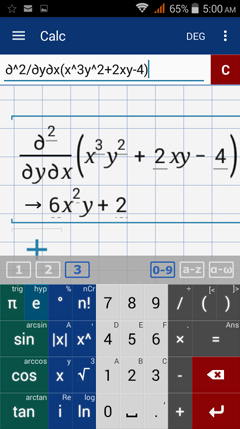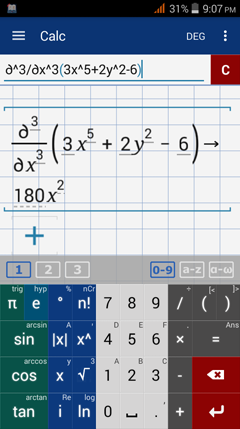17.5. Higher Order Partial Derivatives

Second Order Partial Derivatives

Finding a second order partial derivative allows you to observe multiple changes in the same variable or changes in one variable with respect to another variable. It is similar to taking the second derivative of a derived function but only with respect to the variable of interest, holding the other variables of the first derivative constant.

In a function f(x, y), the following second order partial derivatives can be found:

$f_{xx}=\frac{\partial ^2f}{\partial x\partial x}$

$f_{xy}=\frac{\partial ^2f}{\partial x\partial y}$

$f_{yx}=\frac{\partial ^2f}{\partial y\partial x}$

$f_{yy}=\frac{\partial ^2f}{\partial y\partial y}$

Note: When entering a partial derivative, you don't need to include "f" in the numerator.

Entering Higher Order Partial Derivatives

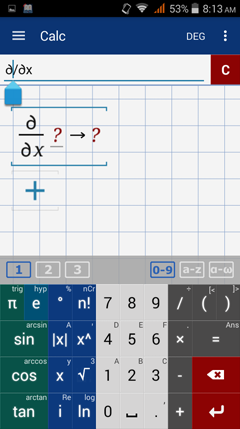
1) Tap and hold the exponent key (x^) and select the partial derivative.

2) Move the cursor right next to δ.
Then enter the order of the partial derivative as an exponent.
Tap the exponent key (x^) followed by the order (2, 3, 4, 5, etc).

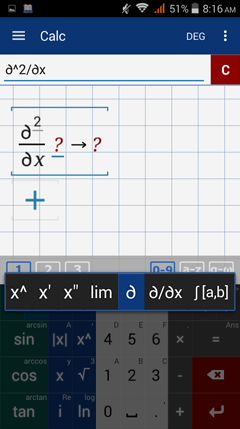
3) Move the cursor to δx to enter the next derivative.
Tap and hold the exponent key (x^) to enter another δ.
Type in the variable of the second partial derivative.

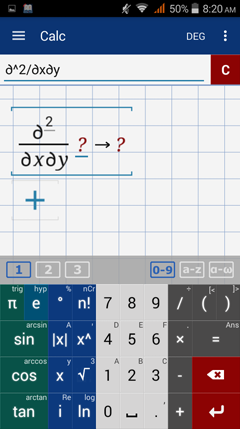
4) Enter the argument in parentheses next to the partial derivative.

Illustrative Example

Calculate the four second order partial derivatives of f(x, y) = 3x^3 y^2.

$f(x,y)=3x^3y^2$

Part 1: Derive the function with respect to x. Then derive it again with respect to x.
First order derivative with respect to x: 9x^2 y^2
Second order derivative with respect to x: 18x y^2

Calculator solution
Use the syntax below.

$\partial ^2/\partial x\partial x\left ( 3x^3y^2 \right )$

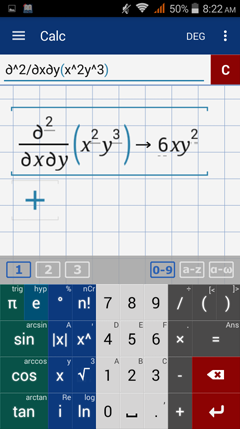
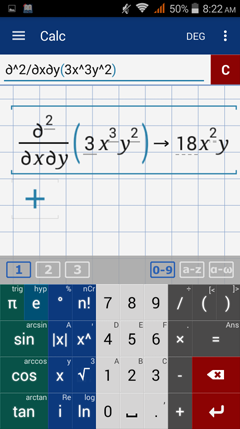
Part 2: Derive the function with respect to x, then derive the result with respect to y.
First order derivative with respect to x: 9x^2 y^2
Second order derivative with respect to y: 18x^2 y

Calculator solution
Use the syntax below.

$\partial ^2/\partial x\partial y\left ( 3x^3y^2 \right )$

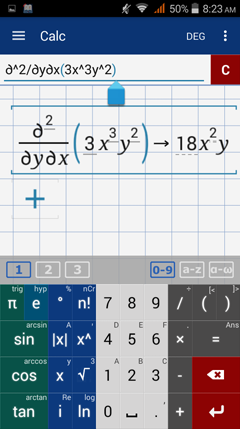
Part 3: Derive the function with respect to y, then derive the result with respect to x.
First order derivative with respect to y: 6x^3 y
Second order derivative with respect to x: 18x^2 y

Calculator solution
Use the syntax below.

$\partial ^2/\partial y\partial x\left ( 3x^3y^2 \right )$

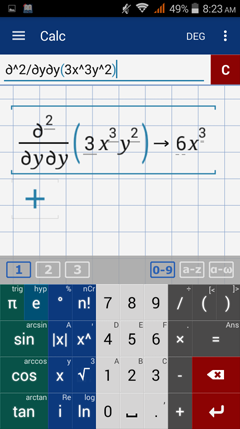
Part 4: Derive the function with respect to y, then derive the result with respect to y again.
First order derivative with respect to y: 6x^3 y
Second order derivative with respect to y: 6x^3

Calculator solution
Use the syntax below.

$\partial ^2/\partial y\partial y\left ( 3x^3y^2 \right )$

More Examples
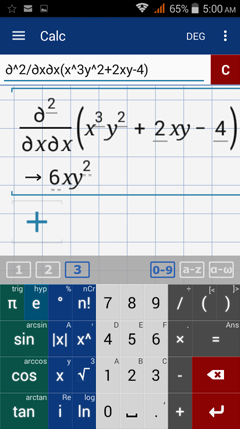
Find the indicated second order partial derivative.

$1)f(x,y)=\textup{cos}\, 2x-x^2e^{5y}+3y^2\, \, ;\: \frac{\partial ^2f}{\partial x\partial y}$

Calculator Syntax:

$\partial ^2/\partial x\partial y\left (\textup{cos}\, 2x-x^2e^{5y}+3y^2 \right )$

$2)f(x,y)=x^3y^2-\frac{4y^6}{x^3}\: \: \: \: \: ;\: \: \frac{\partial ^2f}{\partial x\partial x}$

Calculator Syntax:

$\partial ^2/\partial x\partial x\left (x^3y^2-\frac{4y^6}{x^3} \right )$

$3) z=x^3y^2+2xy-4\; \; ;\; \; \frac{\partial^2 z}{\partial x\partial x}$

Calculator Syntax:

$\partial ^2/\partial x\partial x\left (x^3y^2+2xy-4 \right )$

$4)z=x^3y^2+2xy-4 \; \; \; ;\frac{\partial ^2z}{\partial y\partial x}$

Calculator Syntax:

$\partial ^2/\partial y\partial x\left (x^3y^2+2xy-4 \right )$

Third Order Partial Derivatives

A third order partial derivative is found by deriving a function three times. It adds an additional derivation step to a second order partial derivative.

See the reference below on how to enter a third order partial derivative.

Examples
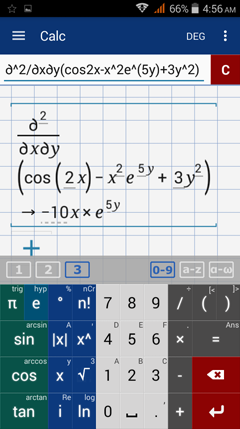
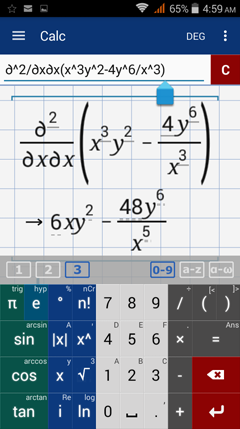
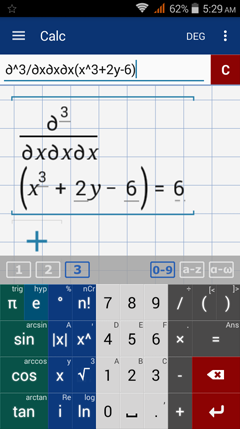
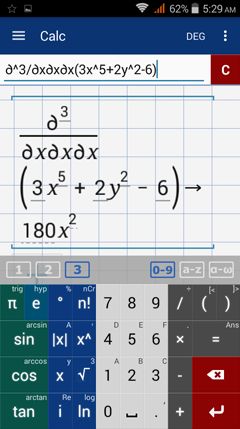
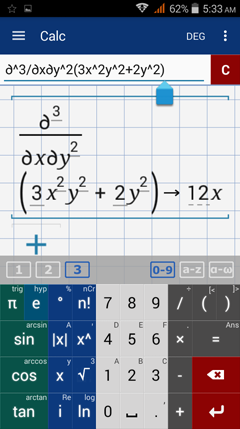
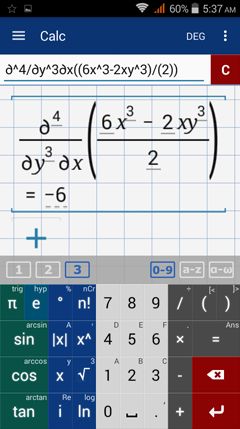
Find the indicated third order partial derivative.

$1) f(x,y)=3x^5+2y^2-6\; \; \; ;\; \frac{\partial ^3z}{\partial x\partial x\partial x}$

Calculator Syntax:

$\partial ^3/\partial x\partial x\partial x\left ( 3x^5+2y^2-6 \right )$

Note: Instead of writing three deltas for the partial derivative, you can also type δx^3.

Calculator Syntax:

$\partial ^3/\partial x^3( 3x^5+2y^2-6 \right))$

$2)f(x,y)=3x^5+2y^4-6\; \; \; \; ;\; \; \; \frac{\partial ^3f}{\partial y\partial y\partial y}$

Calculator Syntax:

$\partial ^3/\partial y\partial y\partial y\left ( 3x^5+2y^4-6 \right )$

$3) z=3x^2y^2+2y^2\: \: \: \: ;\: \: \: \frac{\partial ^3z}{\partial x\partial y^2}$

Calculator Syntax:

$\partial ^3}/{\partial x\partial y^2\left ( 3x^2y^2+2y^2 \right )$

Other Examples

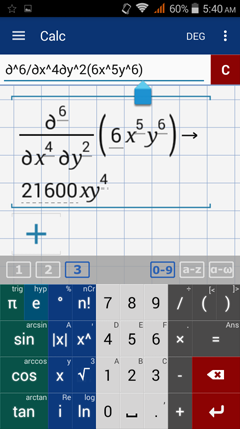
Higher Order Partial Derivatives

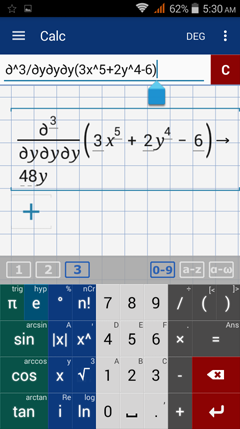
Finding other higher order partial derivative is just like finding the second and third order partial derivatives. Raise δ to the order of the partial derivative (4 for fourth order, 5 for fifth and so on).

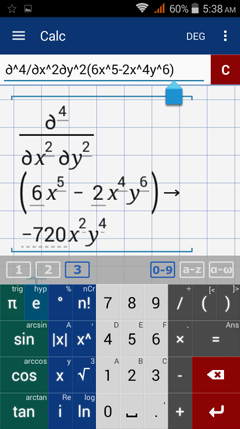
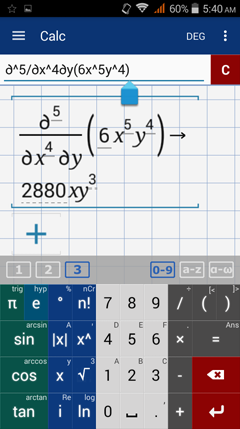
Examples

Find the indicated partial derivative.

$1) f(x,y)=\frac{6x^3-2xy^3}{2}\: \: \: \: ;\; \; \; \frac{\partial ^4f}{\partial y^3\partial x}$