18. Definite Integral
Differentiation is the process of finding the derivative of a function to observe how the function is changing with respect to a change in one of its independent variables. Integration, on the other hand, is the process of converting the derivative back to its original function with the result called the integral. When we calculate the integral of a function, we find the area underneath the curve of the function.
Definite Integral
Definite Integral
Given a function f(x) that is continuous on the interval [a, b] and can be divided into n sub-intervals with equal increments dx, the definite integral of f(x) from a to b is defined as:
Finding the Definite Integral
To find the definite integral of a function f(x),
1) Find the indefinite integral
2) Evaluate the indefinite integral at x = b.
3) Evaluate the indefinite integral at x = a.
4) Subtract the result at x = a from x = b.
Illustrative Example
1) Find the indefinite integral
2) Evaluate the indefinite integral at x = b.
3) Evaluate the indefinite integral at x = a.
4) Subtract the result at x = a from x = b.
Illustrative Example
Calculate the definite integral.
Solution
Step 1: Find the indefinite Integral of (12x^3 - 3x^2 + 4)dx.
Step 1: Find the indefinite Integral of (12x^3 - 3x^2 + 4)dx.
Step 2: Evaluate the indefinite integral at x = 5.
Step 3: Evaluate the indefinite integral at x = 2.
Step 4: Subtract the results.
Calculator Solution
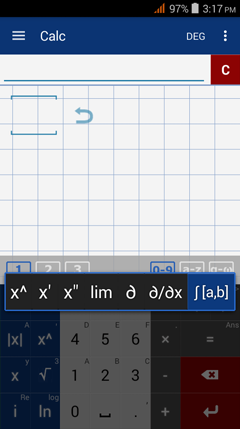
1) Tap and hold the exponent key (x^) and select the integration sign.
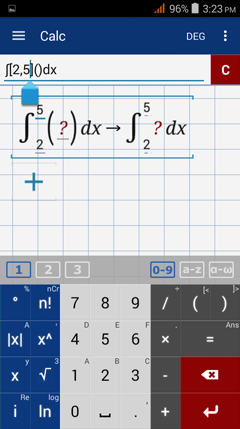
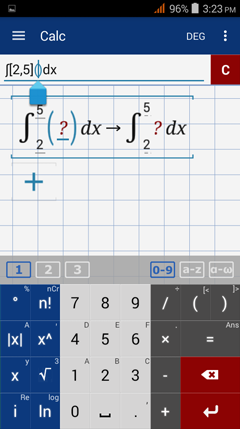
2) Input the upper and lower limits inside the square brackets [a, b].
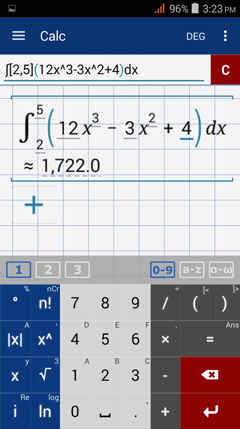
3) Enter the function inside the parentheses.
4) The value of the definite integral will be displayed.
The results are the same as those found manually.