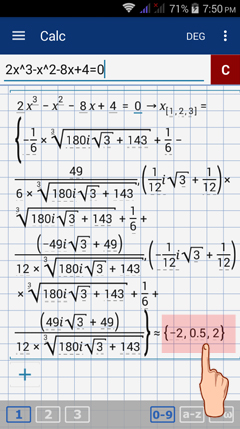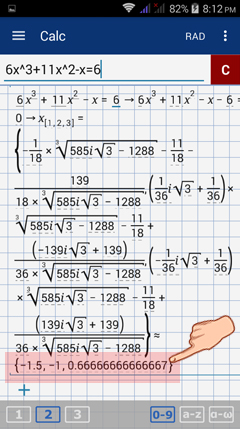8.4. Cubic Equations

A cubic equation is a third degree polynomial. It can be written in the form:

with coefficients a, b, c and d.

Below are some examples of cubic equations:

Solving Cubic Equations

The roots of a cubic equation are the solution to the equation when it equals zero. A cubic equation can have up to three roots and it can be solved by factoring, through a general formula, or by numerical approximation.

Example

Solution by hand
Use the rational root theorem to determine the possible roots of the equation. Since a = 2, and d = 4, then the possible roots are:
+ 4/2,  + 1/2 , + 1/4,  + 1 and + 4. Use synthetic division to solve the cubic equation: 2x^3 - x^2 - 8x + 4 = 0.

-2      /      2            -1            -8                4                       Try x = - 2
                                -4            10              -4
_____________________________________
                  2           -5             2                0                         First factor


2      /      2            -5            2                                            Try x = 2
                                 4           -2
_____________________________________
                 2           -1             0                                             Second factor

So 2x^3 - x^2 - 8x + 4 = 0 can be factored into (x + 2)(x - 2)(2x - 1) = 0
    (x + 2) = 0        x = -2
    (x - 2) = 0        x = 2
    (2x - 1) = 0       x = 1/2
The roots of the equation 2x^3 - x^2 - 8x + 4 = 0 are x = 2, -2, and 1/2.

Calculator solution

Type in the equation 2x^3 - x^2 - 8x + 4 = 0. The roots are displayed automatically. Note: the equation is solved using the general formula.

More Examples

Type in the equation as given: 6x^3 + 11x^2 - x = 6

Type in the equation as given: x^3 = 8

Type in the equation as given: 5x^3 = 625

Type in the equation as given: 4x^3 + 4x^2 - 7x + 2 = 0

next: 8.5. polynomial equation >

list of contents