20.2. Logarithmic Gamma Function
An extension of the gamma function is the logarithmic gamma function, or the log-gamma function.
Because the gamma function of a real number n gives us (n - 1)!, the log-gamma function tells us the logarithm of (n - 1)!.
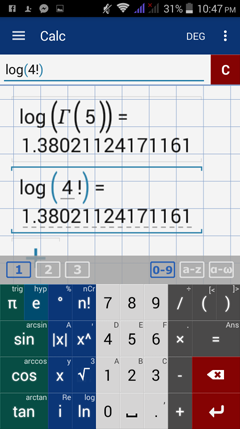
For example, log (gamma (5)) is like finding the common logarithm of 4!, which gives us log(4!) = log (24) as shown below.
Because the gamma function of a real number n gives us (n - 1)!, the log-gamma function tells us the logarithm of (n - 1)!.
For example, log (gamma (5)) is like finding the common logarithm of 4!, which gives us log(4!) = log (24) as shown below.
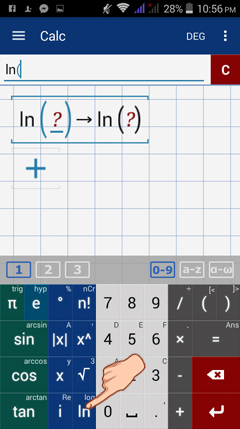
To find the log-gamma function of a number, first select the logarithm (common log, base 2 log, natural log, or base-n log).
Then, enter the gamma function.
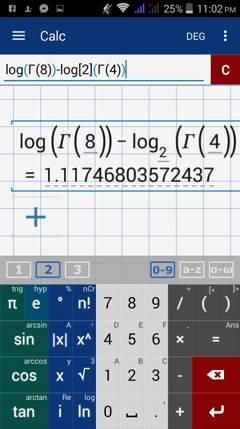
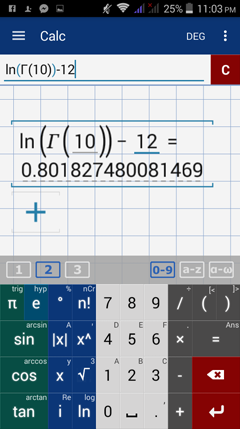
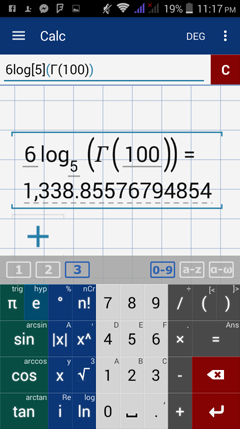
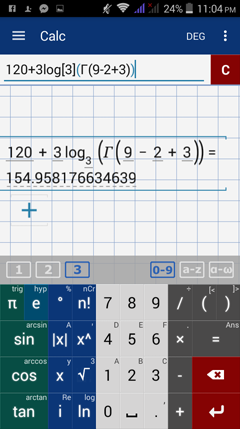
Examples
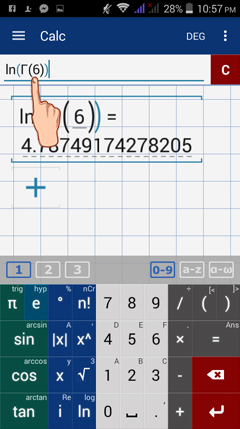
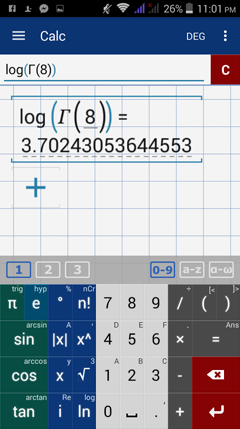
Evaluate each log-gamma function below.
|
Calculator syntax:
|
|
|
Calculator syntax:
|
|
|
Calculator syntax:
|
|
|
Calculator syntax:
|
|
|
Calculator syntax:
|
|
