15.12. Indeterminate Forms
Indeterminate forms are undefined expressions that include: 0/0, a/0, + ∞/0, +∞/+∞, 0( +∞), 1^∞, and ∞^0. They may result from direct substitute when we calculate the limit of a rational function as x approaches c, but it does not mean that the limit doesn't exist.
One way to resolve an indeterminate form is to simplify the given rational expression by factoring the numerator and denominator and canceling common factors. Then we plug c into the reduced rational expression.
Example
Find the limit of f(x) = (x - 1) / (x^2 - 1) as x approaches 1.
Step 1: Check if you can use direct substitution.
- If you plug 1 into f(x), the result is 0/0, so you have to simplify
Step 2: Factor the denominator (x^2 - 1) into (x - 1)(x + 1)
Step 3: Simplify f(x) = (x - 1) / (x - 1)(x + 1) into f(x) = 1/(x + 1)
Step 4: Plug in 1
The limit is f(x) = 1/(1 + 1) = 1/2
One way to resolve an indeterminate form is to simplify the given rational expression by factoring the numerator and denominator and canceling common factors. Then we plug c into the reduced rational expression.
Example
Find the limit of f(x) = (x - 1) / (x^2 - 1) as x approaches 1.
Step 1: Check if you can use direct substitution.
- If you plug 1 into f(x), the result is 0/0, so you have to simplify
Step 2: Factor the denominator (x^2 - 1) into (x - 1)(x + 1)
Step 3: Simplify f(x) = (x - 1) / (x - 1)(x + 1) into f(x) = 1/(x + 1)
Step 4: Plug in 1
The limit is f(x) = 1/(1 + 1) = 1/2
L'Hôpital's Rule
You can also use L'Hôpital's rule to find the limit of a rational function that results in an indeterminate form. The rule says that the limit of a rational function is equal to the limit of the same function after taking the derivative of the numerator and denominator respectively.
You can also use L'Hôpital's rule to find the limit of a rational function that results in an indeterminate form. The rule says that the limit of a rational function is equal to the limit of the same function after taking the derivative of the numerator and denominator respectively.
Example
Find the limit of f(x) = (x - 1) / (x^2 - 1) as x approaches 1.
Step 1: Take the derivative of the numerator
(x - 1)' = 1
Step 2: Take the derivative of the denominator
(x^2 - 1)' = 2x
Step 3: Plug 1 into the limit of f(x) = 1/2x as x approaches 1
f(1) = 1/(2*1) = 1/2
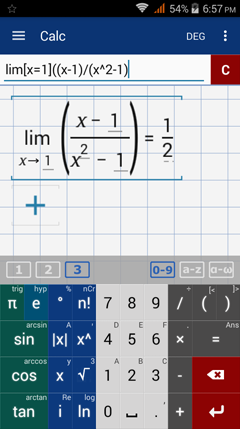
Calculator solution
Type in: lim[x = 1] ((x - 1) / (x^2 - 1))
Find the limit of f(x) = (x - 1) / (x^2 - 1) as x approaches 1.
Step 1: Take the derivative of the numerator
(x - 1)' = 1
Step 2: Take the derivative of the denominator
(x^2 - 1)' = 2x
Step 3: Plug 1 into the limit of f(x) = 1/2x as x approaches 1
f(1) = 1/(2*1) = 1/2
Calculator solution
Type in: lim[x = 1] ((x - 1) / (x^2 - 1))
Case 1: The Limit Exists
To find a limit, you should start by trying to plug c into f(x). If you get an indeterminate form, try something else.
1) Factor the expression.
2) Use L'Hôpital's rule.
3) Test points around c to determine whether the one-sided limits are in the same direction.
4) Graph the function.
Illustrative Example
Calculate the limit.
To find a limit, you should start by trying to plug c into f(x). If you get an indeterminate form, try something else.
1) Factor the expression.
2) Use L'Hôpital's rule.
3) Test points around c to determine whether the one-sided limits are in the same direction.
4) Graph the function.
Illustrative Example
Calculate the limit.
Solution
1) Factor the numerator and denominator.
Factor (x - 1)^2 into (x - 1)(x - 1).
Factor (x^2 - 1) into (x - 1)(x + 1).
2) Cancel out common factors.
The simplified function is f(x) = (x - 1)/(x + 1)
3) Plug 1 into f(x) = (x - 1)/(x + 1)
(x - 1)/( x + 1) = (1 - 1) / (1 + 1) = 0
4) The limit of (x - 1)^2 / (x^2 - 1) as x approaches 1 is 0.
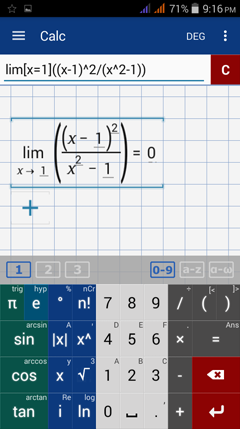
Calculator solution
Type in: lim [ x = 1 ] ( ( x - 1 )^2 / ( x^2 -1 ) )
1) Factor the numerator and denominator.
Factor (x - 1)^2 into (x - 1)(x - 1).
Factor (x^2 - 1) into (x - 1)(x + 1).
2) Cancel out common factors.
The simplified function is f(x) = (x - 1)/(x + 1)
3) Plug 1 into f(x) = (x - 1)/(x + 1)
(x - 1)/( x + 1) = (1 - 1) / (1 + 1) = 0
4) The limit of (x - 1)^2 / (x^2 - 1) as x approaches 1 is 0.
Calculator solution
Type in: lim [ x = 1 ] ( ( x - 1 )^2 / ( x^2 -1 ) )
More Examples
Calculate the limit of each rational function if it exists.
Calculate the limit of each rational function if it exists.
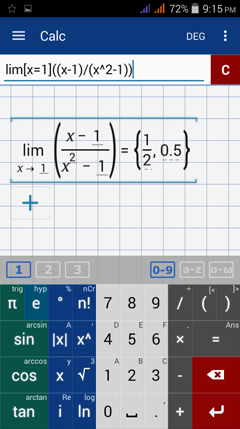
Calculator solution
Type in: lim [ x = 1 ] ( ( x - 1 ) / ( x^2 - 1 ) )
Type in: lim [ x = 1 ] ( ( x - 1 ) / ( x^2 - 1 ) )
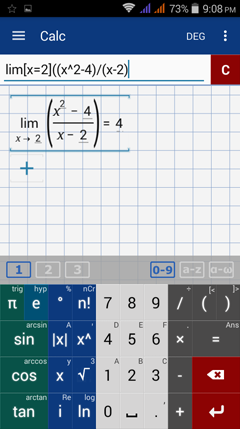
Calculator solution
Type in: lim [ x = 2 ] ( ( x^2 - 4 ) / ( x - 2 ) )
Type in: lim [ x = 2 ] ( ( x^2 - 4 ) / ( x - 2 ) )
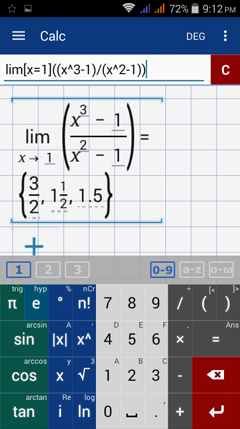
Calculator solution
Type in: lim [ x = 1 ] ( ( x^3 - 1 ) / ( x^2 - 1 ) )
Type in: lim [ x = 1 ] ( ( x^3 - 1 ) / ( x^2 - 1 ) )
Case 2: The Limit Does Not Exist
The limit of a function may not exist if the denominator is zero when we plug in x = c even after factoring and applying L'Hôpital's rule.
Examples
Find each limit if it exists.
Find each limit if it exists.
Step 1: Plug in 1
lim (1^2 - 1)/((1 - 1)^2) = 0/0 indeterminate form
Step 2: Use L'Hôpital's rule
Take the derivative of the numerator (x^2 - 1)' = 2x
Take the derivative of the denominator ((x - 1)^2)' = 2x - 2
Step 3: Find the left- and right-hand limits of (2x/(2x - 2))
a) Left-hand limit
Plug in 0.9999
(2*0.9999)/((2*0.9999) - 2) ≈ 2/(-0.0002) ≈ -∞ since the denominator is almost zero but is negative
b) Right-hand limit
Plug in 1.0001
(2*1.0001)/((2*1.0001) - 2) ≈ 2/(0.0002) ≈ ∞ since the denominator is almost zero but is positive
Step 4: The left- and right-hand limits are not in the same direction (one goes to negative infinity and the other to positive infinity), so the limit does not exist.
lim (1^2 - 1)/((1 - 1)^2) = 0/0 indeterminate form
Step 2: Use L'Hôpital's rule
Take the derivative of the numerator (x^2 - 1)' = 2x
Take the derivative of the denominator ((x - 1)^2)' = 2x - 2
Step 3: Find the left- and right-hand limits of (2x/(2x - 2))
a) Left-hand limit
Plug in 0.9999
(2*0.9999)/((2*0.9999) - 2) ≈ 2/(-0.0002) ≈ -∞ since the denominator is almost zero but is negative
b) Right-hand limit
Plug in 1.0001
(2*1.0001)/((2*1.0001) - 2) ≈ 2/(0.0002) ≈ ∞ since the denominator is almost zero but is positive
Step 4: The left- and right-hand limits are not in the same direction (one goes to negative infinity and the other to positive infinity), so the limit does not exist.
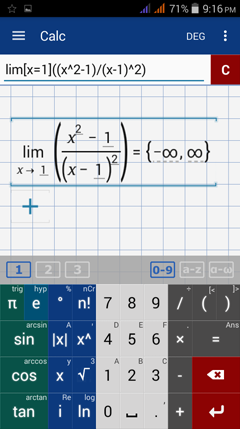
Calculator solution
Type in: lim [ x = 1 ] ( ( x^2 - 1 ) / ( x - 1 )^2 )
Type in: lim [ x = 1 ] ( ( x^2 - 1 ) / ( x - 1 )^2 )
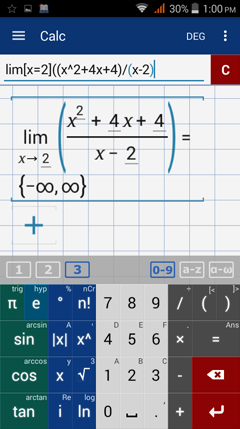
Calculator solution
Type in: lim [ x=2 ] ( ( x^2 + 4x + 4 ) / ( x-2 ) )
Type in: lim [ x=2 ] ( ( x^2 + 4x + 4 ) / ( x-2 ) )
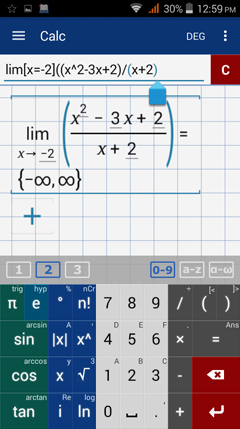
Calculator solution
Type in: lim [ x = -2 ] ( ( x^2 - 3x + 2 ) / ( x+2 ) )
Type in: lim [ x = -2 ] ( ( x^2 - 3x + 2 ) / ( x+2 ) )