15.7. Limit of an Absolute Value Function

The absolute value of a number is the distance of the number from zero, meaning that the absolute values of 6 and -6 are 6.
An absolute value function is defined as:

$\left | a \right |=\left\{\begin{matrix} a & if \ a>0\\ -a& if \ a<0 \end{matrix}\right.$

Limit of an Absolute Value Function as x Approaches a Real Number c
Because the argument of an absolute value function may be positive or negative, we have to satisfy both cases: when x > 0 and x < 0.

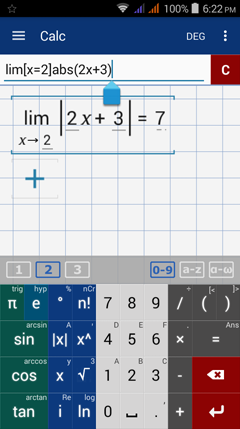
Suppose we want to find the limit of |2x + 3| as x approaches 2 as follows:

$\lim_{x\rightarrow 2}\left | 2x+3 \right |$

To calculate the limit, we have to separate the absolute value into two cases:

Case 1: 2x + 3 if 2x + 3 > 0
Case 2: -(2x + 3) if 2x + 3 < 0

$\left | 2x+3 \right |=\left\{\begin{matrix} 2x+3 & if x \geq -3/2\\ -(2x+3)& if x< -3/2 \end{matrix}\right.$

Because we are looking for the limit as x approaches 2, it falls into the first case since 2 > -3/2. Therefore to find the limit, we have to plug 2 using |2x + 3|. The limit is |2*2 + 3| = 7.

More Examples
Find the limit of each absolute value function if it exists.

$1) \lim_{x\rightarrow 4}\left | 2x+3 \right |-3$

Calculator solution
Type in: lim [ x = 4 ] abs( 2x + 3 ) - 3

Case 1: 2x + 3 if 2x + 3 > 0 or x > -3/2
Case 2: -(2x + 3) if 2x + 3 < 0 or x < -3/2

Since 4 > - 3/2, we evaluate the expression 2x + 3 at x = 4.
|2(4) + 3| - 3 = 11 - 3 = 8.

$2) \lim_{x\rightarrow -3}(\left | x+1\right |+\frac{3}{x})$

Calculator solution
Type in: lim [ x = -3 ] ( ( abs( x + 1 ) + 3 / x )

Case 1: x + 1 if x > - 1
Case 2: -(x + 1) if x < -1

Since -3 < - 1, we evaluate -(x + 1) at x = -3.
-(-3 + 1) + 3/(-3) = -(-2) - 1 = 2 - 1 = 1.

$3) \lim_{x\rightarrow 3}(2(\left | x^2-4\right |-\left | x \right |-4))$

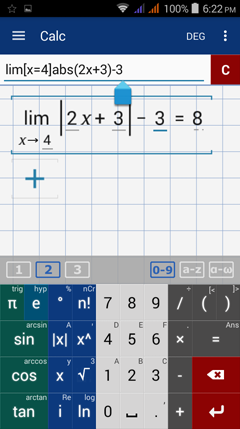
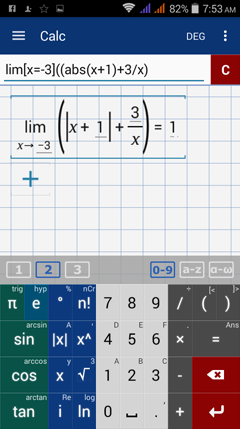
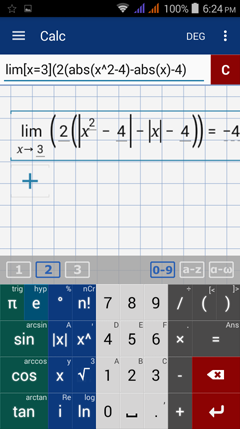
Calculator solution
Type in: lim [ x = 3 ] ( 2 ( abs( x^2 - 4 ) - abs( x ) - 4 ) )

$4) \lim_{x\rightarrow 2^-}(\frac{x^2+x-6}{\left | x-2 \right |})$

Calculator solution
Type in: lim [ x = 2 - ] ( ( x^2 + x - 6 ) / abs( x - 2 ) )

next: 15.8. limit of a trigonometric function >

list of contents