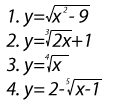11.9. Radical Functions
A radical function expresses the independent variable as the radicand. Enter a radical function using the root key and enclose the radicand inside parentheses.
To graph a radical function:
1) If the equation is defined explicitly i.e. "y =," enter only the radical expression.
2) If the equation is defined implicitly, enter the entire equation as given.
3) To sketch graphs on the same coordinate axes, enter one equation per line.
Examples
Sketch the graphs of the following radical functions:
To graph a radical function:
1) If the equation is defined explicitly i.e. "y =," enter only the radical expression.
2) If the equation is defined implicitly, enter the entire equation as given.
3) To sketch graphs on the same coordinate axes, enter one equation per line.
Examples
Sketch the graphs of the following radical functions:
Calculator solutions
Use the square root key or type "root" using the a-z keyboard. Enter the index in brackets [ ] and the argument in parentheses. For a cube root, tap the square root key twice, and for a 4th root, tap the square root key three times.
1) Enter the expression: sqrt(x^2 - 9). Use the exponent key x^n to enter the exponent. Hit enter to go to the next line.
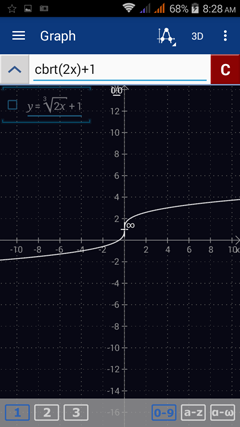
2) Enter the expression: cbrt(2x) + 1. Hit enter.
3) Enter the expression: root[4](x). Hit enter.
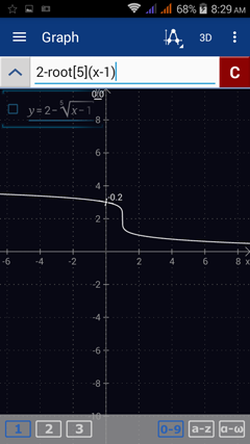
4) Enter the expression: 2 - root[5](x - 1).
Use the square root key or type "root" using the a-z keyboard. Enter the index in brackets [ ] and the argument in parentheses. For a cube root, tap the square root key twice, and for a 4th root, tap the square root key three times.
1) Enter the expression: sqrt(x^2 - 9). Use the exponent key x^n to enter the exponent. Hit enter to go to the next line.
2) Enter the expression: cbrt(2x) + 1. Hit enter.
3) Enter the expression: root[4](x). Hit enter.
4) Enter the expression: 2 - root[5](x - 1).
To look at each graph individually, enter one equation per workspace.
1) sqrt(x^2 - 9)

2) cbrt(2x) + 1
3) root[4](x)
4) 2 - root[5](x - 1)