15.11. Limit at Infinity
Polynomial Functions
Finding the limit of a polynomial function at infinity is the same as finding the limit as x approaches +∞. Similarly, the limit at negative infinity is the same as finding the limit as x approaches -∞. If f(x) increases as x increases then the limit of f(x) as x approaches +∞ is +∞. If f(x) decreases as x approaches -∞, then the limit of f(x) as x approaches -∞ is -∞.
You can determine the limit of a function as it approaches -∞ or +∞ based on its degree (the highest exponent).
1) When the degree is odd, such as f(x) = x or f(x) = x^3
Case 1: a > 0
The limit at +∞ is +∞.
The limit at -∞ is -∞.
Case 2: a < 0
The limit at +∞ is -∞.
The limit at -∞ is +∞.
2) When the degree is even, such as f(x) = x^2 or f(x) = x^4
Case 1: a > 0
The limit at +∞ is +∞.
The limit at -∞ is +∞.
Case 2: a < 0
The limit at +∞ is -∞.
The limit at -∞ is -∞.
You can determine the limit of a function as it approaches -∞ or +∞ based on its degree (the highest exponent).
1) When the degree is odd, such as f(x) = x or f(x) = x^3
Case 1: a > 0
The limit at +∞ is +∞.
The limit at -∞ is -∞.
Case 2: a < 0
The limit at +∞ is -∞.
The limit at -∞ is +∞.
2) When the degree is even, such as f(x) = x^2 or f(x) = x^4
Case 1: a > 0
The limit at +∞ is +∞.
The limit at -∞ is +∞.
Case 2: a < 0
The limit at +∞ is -∞.
The limit at -∞ is -∞.
Illustrative Example
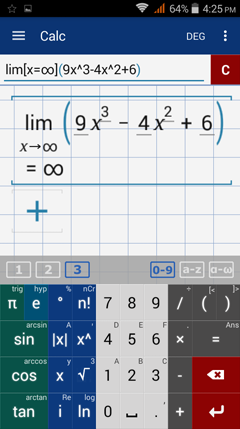
Find the limit of f(x) = x^3 - 4x^2 + 6 as x approaches -∞.
This is a 3rd degree polynomial with a = 1 > 0. So the limit as x approaches -∞ is -∞.
Calculator solution
Step 1: Tap and hold the exponent key. Select "lim." You can also tap the exponent key four times.
Calculator solution
Step 1: Tap and hold the exponent key. Select "lim." You can also tap the exponent key four times.
Step 2: Enter infinity by holding the degree key and selecting ∞. You can also tap the degree key four times.
Step 3: Enter the function in parentheses.
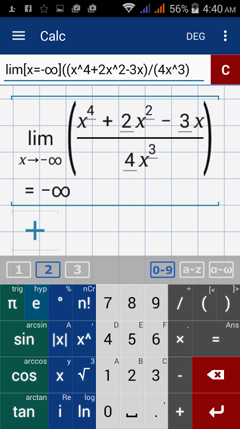
Type in: lim [ x = -∞ ] ( 9x^3 - 4x^2 + 6 )
Type in: lim [ x = -∞ ] ( 9x^3 - 4x^2 + 6 )
More Examples
Find the limit at infinity for each polynomial function below.
Calculator solution
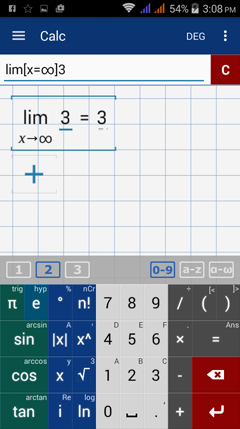
Type in: lim [ x = ∞ ] 3
Type in: lim [ x = ∞ ] 3
Calculator solution
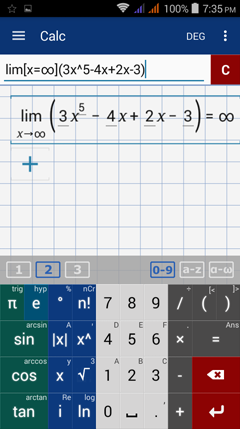
Type in: lim [ x = ∞ ] ( 3x^5 - 4x + 2x - 3 )
Type in: lim [ x = ∞ ] ( 3x^5 - 4x + 2x - 3 )
Calculator solution
Type in: lim [ x = - ∞ ] ( -3x^4 - 4x^3 + 2x - 3 )
Type in: lim [ x = - ∞ ] ( -3x^4 - 4x^3 + 2x - 3 )
Calculator solution
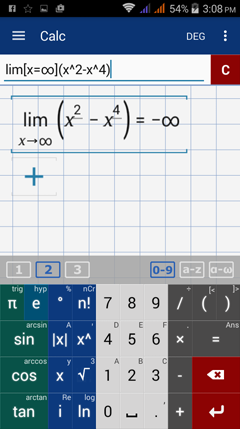
Type in: lim [ x = ∞ ] ( x^2 - x^4 )
Type in: lim [ x = ∞ ] ( x^2 - x^4 )
Rational Functions
To find the limit at infinity of a rational function, let ax^n be the first term of the numerator and bx^m be the first term of the denominator.
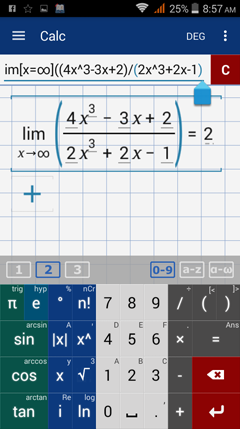
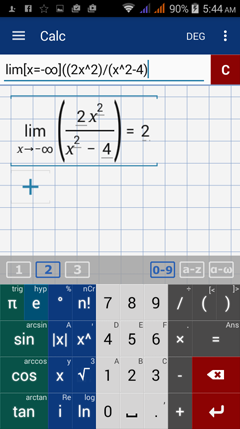
1) If the degree of the numerator is equal to the degree of the denominator, the limit at infinity is a/b. In the example below, the degrees are the same ( x^3 ), so the limit at infinity is 4/2 = 2.
1) If the degree of the numerator is equal to the degree of the denominator, the limit at infinity is a/b. In the example below, the degrees are the same ( x^3 ), so the limit at infinity is 4/2 = 2.
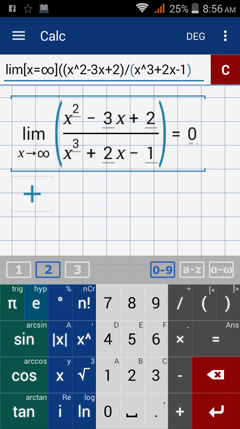
2) If the degree of the numerator is less than the degree of the denominator, then the limit at infinity is 0. In the example below, the degree of the numerator is x^2 which is less than the degree of the denominator x^3, so the limit is 0.
3) If the degree of the numerator is greater than the denominator, the limit is either positive or negative infinity.
More Examples
Calculate the limit at infinity for each rational function below.
Calculator solution
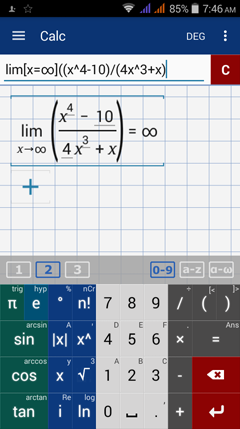
Type in: lim [ x = ∞ ] ( ( x^4 - 10 ) / ( 4x^3 + x ) )
Type in: lim [ x = ∞ ] ( ( x^4 - 10 ) / ( 4x^3 + x ) )
Calculator solution
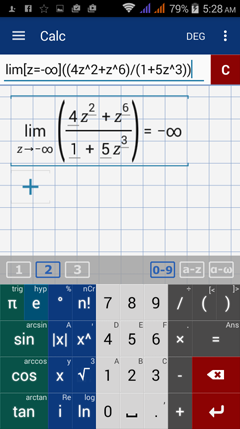
Type in: lim [ z = -∞ ] ( ( 4z^2 + z ^ 6 ) / ( 1 + 5z^3 ) )
Type in: lim [ z = -∞ ] ( ( 4z^2 + z ^ 6 ) / ( 1 + 5z^3 ) )
Calculator solution
Type in: lim [ x = -∞ ] ( ( 2x^2 ) / ( x^2 - 4 ) )
Type in: lim [ x = -∞ ] ( ( 2x^2 ) / ( x^2 - 4 ) )
Calculator solution
Type in: lim [ x = ∞ ] ( ( 4x^3 ) / ( 5x^2 - 3 ) )
Type in: lim [ x = ∞ ] ( ( 4x^3 ) / ( 5x^2 - 3 ) )
Calculator solution
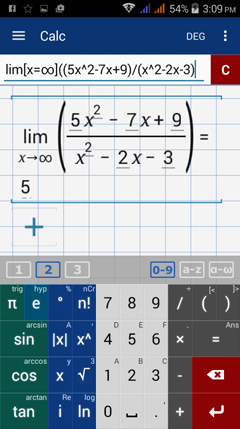
Type in: lim [ x = ∞ ] ( ( 5x^2 - 7x + 9 ) / ( x^2 -2x - 3 ) )
Type in: lim [ x = ∞ ] ( ( 5x^2 - 7x + 9 ) / ( x^2 -2x - 3 ) )
Calculator solution
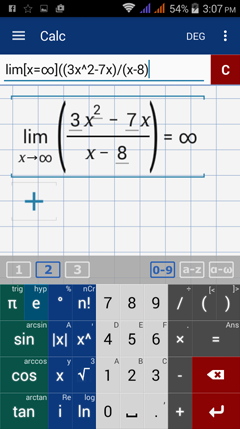
Type in: lim [ x = ∞ ] ( ( 3x^2 - 7x ) / ( x - 8 ) )
Type in: lim [ x = ∞ ] ( ( 3x^2 - 7x ) / ( x - 8 ) )
Radical Functions
To find the limit at infinity of a radical function, you can substitute large values of x to see the behavior of the function f(x). The limit also depends on the degree of the radical and the radicand. If the radicand contains a fraction, the rules for rational expressions hold.
Illustrative Examples
Illustrative Examples
Calculate the limit at infinity for each radical function below.
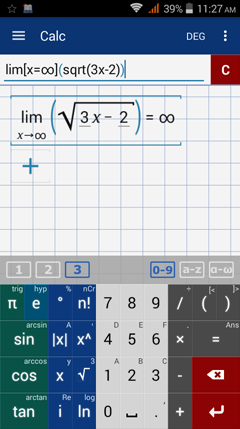
As x increases, the value of sqrt(3x - 2) increases. So the limit is +∞.
The domain of the radical function is the set of real numbers greater than or equal to 3/2, so the limit as x approaches -∞ does not exist.
The function is positive for any x, so plugging in a large negative number into f(x) would result in a large positive number. The limit is +∞.
More Examples
Calculate each limit at infinity below.
Calculate each limit at infinity below.
Calculator solution
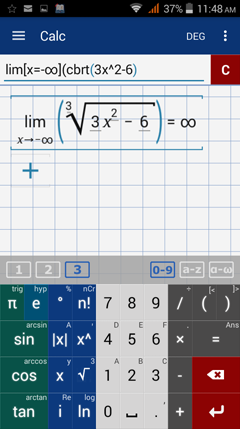
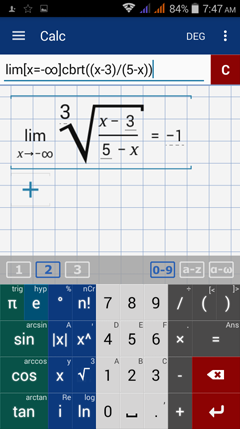
Type in: lim [ x = -∞ ] cbrt( ( x - 3 ) / ( 5 - x ) )
Type in: lim [ x = -∞ ] cbrt( ( x - 3 ) / ( 5 - x ) )
Calculator solution
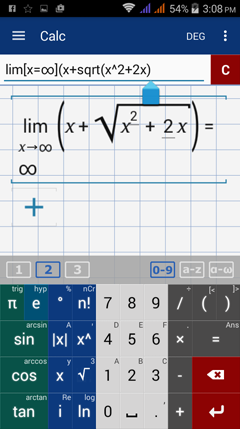
Type in: lim [ x = ∞ ] ( x + sqrt( x^2 + 2x ) )
Type in: lim [ x = ∞ ] ( x + sqrt( x^2 + 2x ) )
Calculator solution
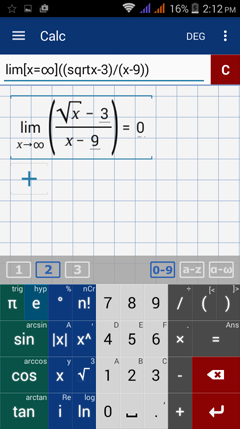
Type in: lim [ x = ∞ ] ( ( sqrt x - 3 ) / ( x - 9 ) )
Type in: lim [ x = ∞ ] ( ( sqrt x - 3 ) / ( x - 9 ) )
Calculator solution
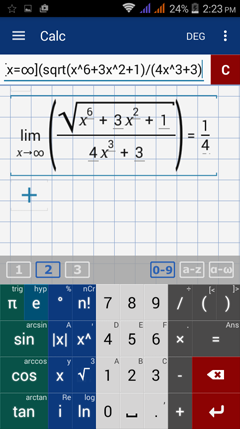
Type in: lim [ x = ∞ ] ( sqrt( x^6 + 3x^2 + 1 ) / ( 4x^3 + 3 ) )
Type in: lim [ x = ∞ ] ( sqrt( x^6 + 3x^2 + 1 ) / ( 4x^3 + 3 ) )
Calculator solution
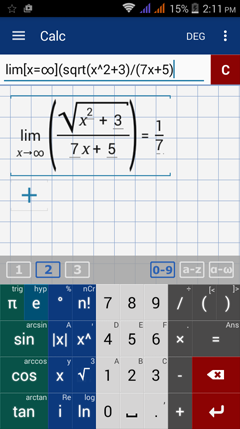
Type in: lim [ x = ∞ ] ( sqrt( x^2 + 3 ) / ( 7x + 5 ) )
Type in: lim [ x = ∞ ] ( sqrt( x^2 + 3 ) / ( 7x + 5 ) )
Absolute Value Functions
The graph of an absolute value function may increase or decrease at all values of x depending on whether it opens upward or downward.
Examples
Calculate each limit at infinity if it exists.
Calculate each limit at infinity if it exists.
Calculator solution
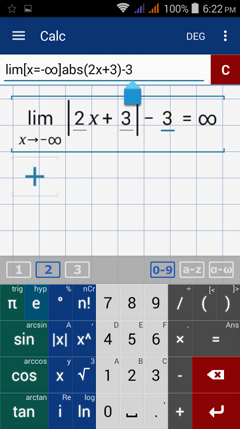
Type in: lim [ x = -∞ ] abs ( 2x + 3 ) - 3
Type in: lim [ x = -∞ ] abs ( 2x + 3 ) - 3
Calculator solution
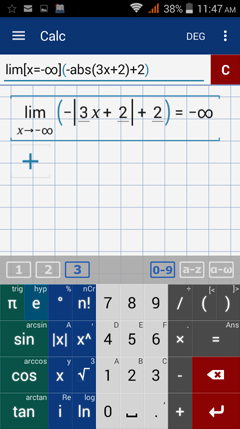
Type in: lim [ x = -∞ ] ( -abs ( 3x + 2 ) + 2 )
Type in: lim [ x = -∞ ] ( -abs ( 3x + 2 ) + 2 )
Calculator solution
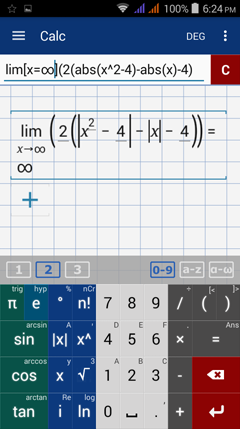
Type in: lim [ x = ∞ ] (2 ( abs( x^2 - 4 ) - abs( x ) - 4 ) )
Type in: lim [ x = ∞ ] (2 ( abs( x^2 - 4 ) - abs( x ) - 4 ) )
Calculator solution
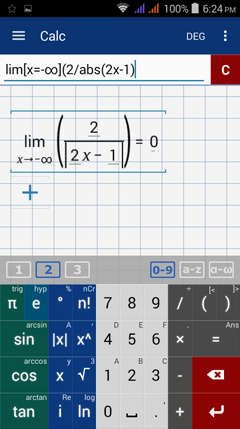
Type in: lim [ x = -∞ ] ( 2 / abs( 2x - 1 ) )
Type in: lim [ x = -∞ ] ( 2 / abs( 2x - 1 ) )
Calculator solution
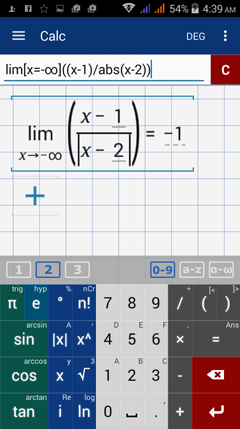
Type in: lim [ x = -∞ ] ( ( x - 1 ) / abs( x - 2 ) )
Type in: lim [ x = -∞ ] ( ( x - 1 ) / abs( x - 2 ) )
Exponential Functions
An exponential function with a base b > 1 has a graph that increases as x increases, so the limit at positive infinity is +∞. Note that an exponential function f(x) = b^x also has an asymptote. The asymptote is the limit at negative infinity.
When 0 < b < 1, the reverse is true. The limit at positive infinity is the y-value of the asymptote while the limit at negative infinity is +∞.
Illustrative Examples
When 0 < b < 1, the reverse is true. The limit at positive infinity is the y-value of the asymptote while the limit at negative infinity is +∞.
Illustrative Examples
Calculate each limit at infinity.
Since b = 3 > 1, the limit at infinity is +∞.
Since b = 1/2 < 1, f(x) approaches the asymptote y = 3. The limit at positive infinity is 3.
More Examples
Calculate each limit below if it exists.
Calculate each limit below if it exists.
Calculator solution
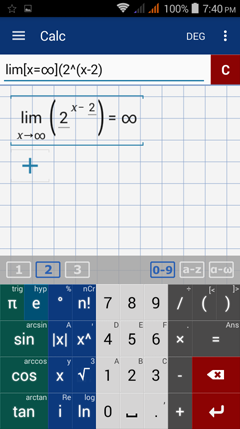
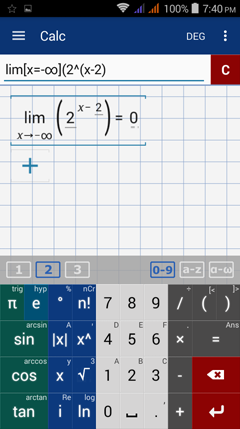
Type in: lim [ x = ∞ ] ( 2^( x - 2 ) )
Type in: lim [ x = ∞ ] ( 2^( x - 2 ) )
Calculator solution
Type in: lim [ x = -∞ ] ( 2^( x - 2 ) )
Type in: lim [ x = -∞ ] ( 2^( x - 2 ) )
Calculator solution
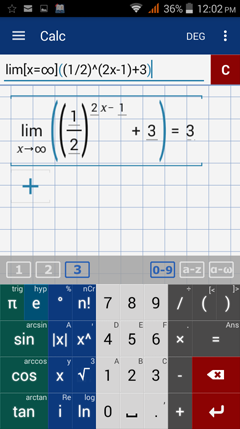
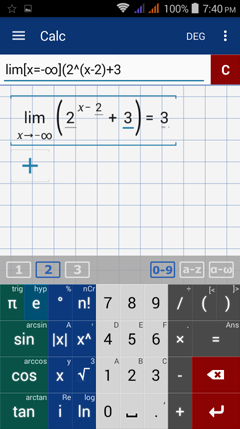
Type in: lim [ x = -∞ ] ( 2 ^( x - 2 ) + 3 )
Type in: lim [ x = -∞ ] ( 2 ^( x - 2 ) + 3 )
Calculator solution
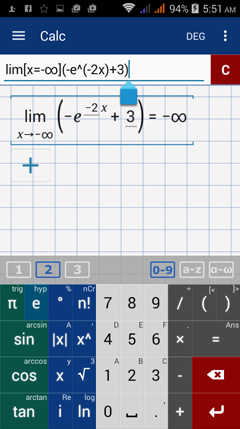
Type in: lim [ x = -∞ ] ( -e^( -2x ) + 3 )
Type in: lim [ x = -∞ ] ( -e^( -2x ) + 3 )
Logarithmic Functions
A logarithmic function is the inverse of an exponential function. Since the range of an exponential function is the set of real numbers greater than zero, the domain of a logarithmic function is the set of real numbers greater than zero. Therefore evaluating limits at negative infinity is not possible. A logarithmic function also has a vertical asymptote. The expression and base of the logarithmic function determine whether it approaches negative or positive infinity.
Illustrative Examples
Illustrative Examples
Calculate each limit at infinity if it exists.
As x increases, f(x) increases, so the limit is +∞.
Because the domain must be positive, the limit at negative infinity is undefined.
More Examples
Calculate each limit at infinity if it exists.
Calculator solution
Type in: lim [ x = ∞ ] log ( 2x )
Type in: lim [ x = ∞ ] log ( 2x )
Calculator solution
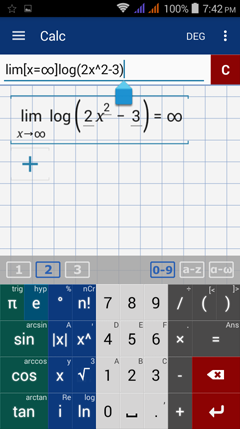
Type in: lim [ x = ∞ ] log ( 2x^2 - 3 )
Type in: lim [ x = ∞ ] log ( 2x^2 - 3 )
Calculator solution
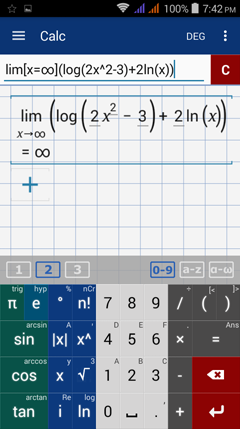
Type in: lim [ x = ∞ ] ( log ( 2x^3 - 3 ) + 2 ln x )
Type in: lim [ x = ∞ ] ( log ( 2x^3 - 3 ) + 2 ln x )
Calculator solution
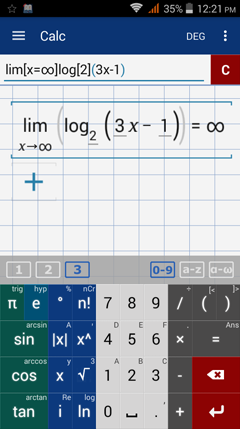
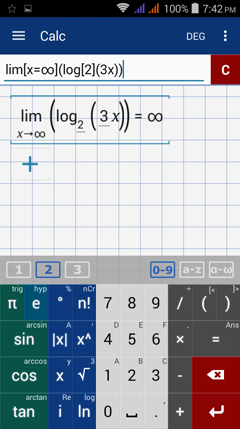
Type in: lim [ x = ∞ ] log [2] ( 3x )
Type in: lim [ x = ∞ ] log [2] ( 3x )
Calculator solution
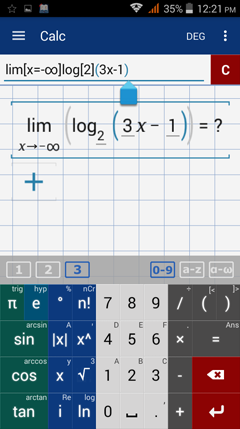
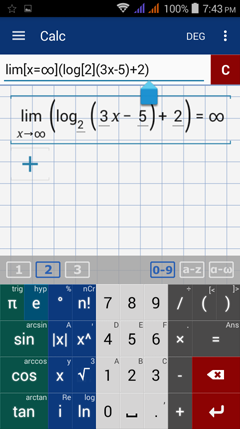
Type in: lim [ x = ∞ ] ( log [2] ( 3x - 5 ) + 2 )
Type in: lim [ x = ∞ ] ( log [2] ( 3x - 5 ) + 2 )
Trigonometric Functions
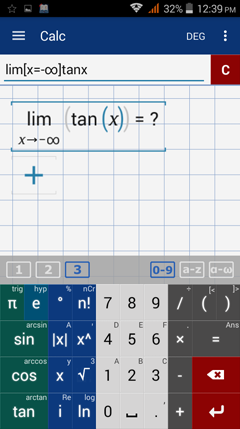
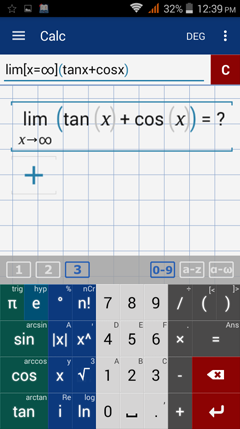
Since most trigonometric functions are periodic (oscillating), limits at infinity do not exist except when the trigonometric expressions are part of an algebraic expression.
Illustrative Examples
Illustrative Examples
Calculate each limit at infinity below.
More Examples
Calculate each limit at infinity if it exists.
Calculate each limit at infinity if it exists.
Calculator solution
Type in: lim [ x = ∞ ] ( ( 2x ) / cos ( 1 / x ) )
Type in: lim [ x = ∞ ] ( ( 2x ) / cos ( 1 / x ) )
Calculator solution
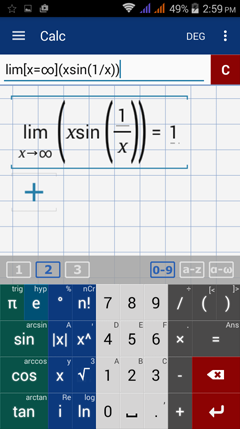
Type in: lim [ x = ∞ ] ( x sin ( 1 / x ) )
Type in: lim [ x = ∞ ] ( x sin ( 1 / x ) )
Functions with No Limit at x = c
Some functions oscillate as x increases such that the limit at infinity does not exist.
Examples
Examples
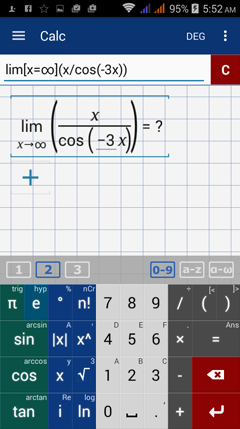
Calculator solution
Type in: lim [ x = ∞ ] ( x / cos ( -3x ) )
Type in: lim [ x = ∞ ] ( x / cos ( -3x ) )
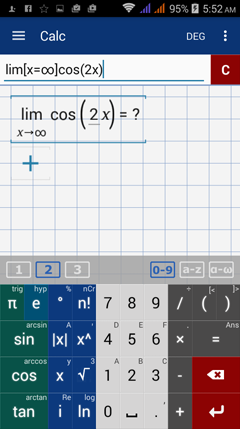
Calculator solution
Type in: lim [ x = ∞ ] cos ( 2x )
Type in: lim [ x = ∞ ] cos ( 2x )
Calculator solution
Type in: lim [ x = -∞ ] log ( 2x - 3 )
Type in: lim [ x = -∞ ] log ( 2x - 3 )
Calculator solution
Type in: lim [ x = -∞ ] log [2] ( 3x )
Type in: lim [ x = -∞ ] log [2] ( 3x )