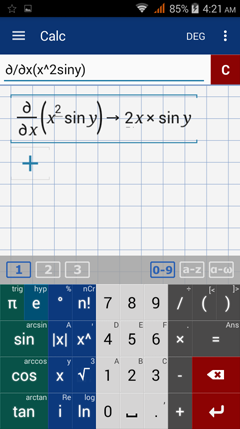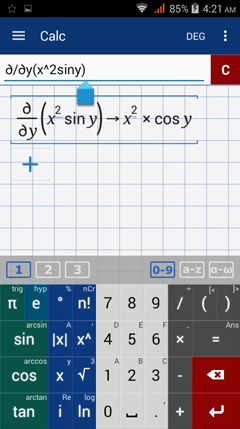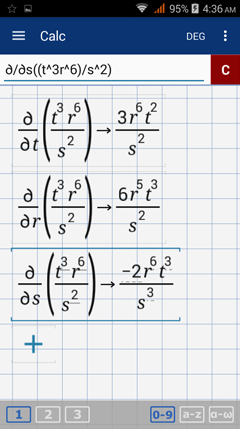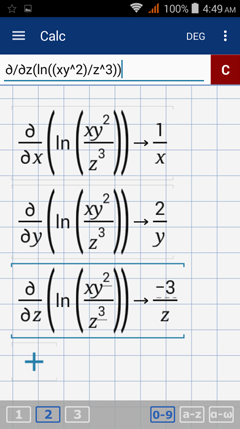17.4. Other Partial Derivatives
Given a function f(x), f '(x) is the rate of change of f(x). The partial derivative describes the change in f(x) due to changes in x and y.
First Order Partial Derivatives
This section focuses on cases where only one variable changes while the others are held fixed. For example, if f(x, y) = 3x^3 y^2, the partial derivative with respect to x refers to the effect of a change in x on f(x,y) holding y constant. This means that to take the derivative, you would treat x as a variable and y as a constant. Similarly, the partial derivative with respect to y refers to the effect of a change in y on f(x,y) holding x constant.
Suppose we let z = f(x, y), then the following first order partial derivatives can be found:
First Order Partial Derivatives
This section focuses on cases where only one variable changes while the others are held fixed. For example, if f(x, y) = 3x^3 y^2, the partial derivative with respect to x refers to the effect of a change in x on f(x,y) holding y constant. This means that to take the derivative, you would treat x as a variable and y as a constant. Similarly, the partial derivative with respect to y refers to the effect of a change in y on f(x,y) holding x constant.
Suppose we let z = f(x, y), then the following first order partial derivatives can be found:
Because f(x,y) has two independent variables, we have two partial derivatives.
Illustrative Example
The partial derivatives are as follows:
|
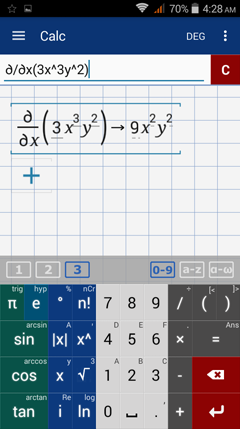
To find the partial derivative with respect to x, we use the power rule on the x term, 3x^3, to get 9x^2. Because y^2 is a constant, the partial derivative is 9x^2 y^2.
To find the partial derivative with respect to y, we use the power rule on the y term, y^2, to get 2y. Since x^3 is a constant, the partial derivative is 2y * 3 * x^3 = 6x^3 y.
|
Calculator Solution
Part 1: Solve for the partial derivative with respect to x.
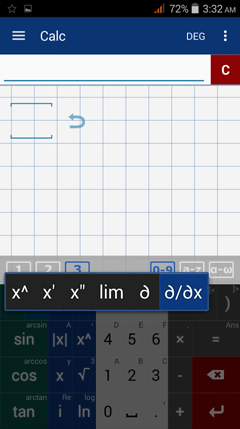
1) Hold the exponent key (x^) and select the partial derivative key.
1) Hold the exponent key (x^) and select the partial derivative key.
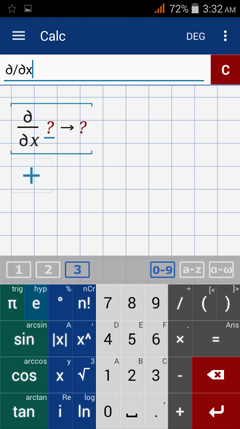
2) Type in the given function next to the partial derivative.
3) Make sure to enter the function in parentheses.
The result is understood as 9x^2y^2 dx.
Part 2: Solve for the partial derivative with respect to y.
Use the same workspace to solve for the partial derivative of f(x, y) in terms of y. Since you've already entered the partial derivative in terms of x, you can do the following:
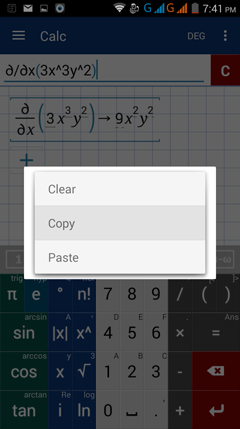
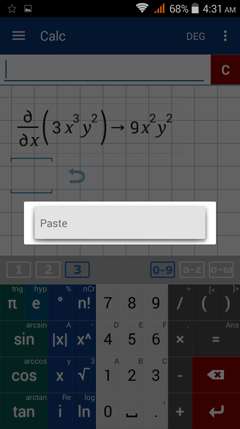
4) Tap and hold the input field to view the "clear, copy, and paste" options. Then tap "copy."
Use the same workspace to solve for the partial derivative of f(x, y) in terms of y. Since you've already entered the partial derivative in terms of x, you can do the following:
4) Tap and hold the input field to view the "clear, copy, and paste" options. Then tap "copy."
5) Hit the enter key. Tap and hold the new input field to see "paste." Tap "paste."
6) The copied equation now appears in the same workspace area.
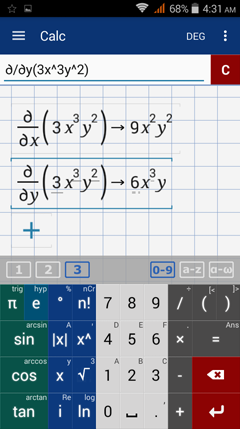
Bring the cursor to the "x" in the partial derivative. Delete "x" and replace it with "y."
The partial differential of f(x, y) is now in terms of y. It is understood as 6x^3 y dy.
More Examples
Find all first order partial derivatives of each function below.
Find all first order partial derivatives of each function below.
The partial derivative of f(x,y) with respect to x is 2x sin y dx.
The partial derivative of f(x,y) with respect to y is x^2 cos y dy.
The first order partial derivatives are:
With respect to t: (t^3r^6 t^2)/s^2 dt
With respect to r: (6r^5 t^3)/s^2 dr
With respect to s: (-2r^6 t^3)/s^3 ds
With respect to t: (t^3r^6 t^2)/s^2 dt
With respect to r: (6r^5 t^3)/s^2 dr
With respect to s: (-2r^6 t^3)/s^3 ds
The first order partial derivatives are:
The first order partial derivatives are:
With respect to x: 1/x dx
With respect to y: 2/y dy
With respect to z: -3/z dz
With respect to x: 1/x dx
With respect to y: 2/y dy
With respect to z: -3/z dz