6.13. Complex Numbers
The set of complex numbers refers to the set of real and imaginary numbers. Any complex number can be written in the form a + bi, where a represents the real number part and bi represents the imaginary number part. In algebra, i is used to denote the square root of -1. Hence i^2 is equal to -1.
Imaginary Number Key (i)
Other keys available on this button: Re, Im, conj, arg.
Tap the i key once to use the imaginary number (i) key. Use this key when performing operations on complex numbers.
Examples
Simplify the following.
Imaginary Number Key (i)
Other keys available on this button: Re, Im, conj, arg.
Tap the i key once to use the imaginary number (i) key. Use this key when performing operations on complex numbers.
Examples
Simplify the following.
1. (2 – 3i) + (6 + 4i)
2. (2 – 3i) (6 + 4i)
| 3. | (2 – 3i) (6 + 4i) |
| 3 + 5i |
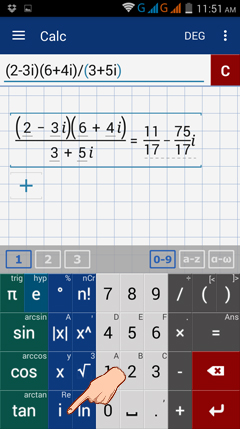
Calculator solutions
Type the expression as it appears with one on each line.
1) Type: (2-3i) + (6+4i)
2) Type: (2-3i)(6+4i)
3) Type: (2-3i)(6+4i) / (3+5i)
Type the expression as it appears with one on each line.
1) Type: (2-3i) + (6+4i)
2) Type: (2-3i)(6+4i)
3) Type: (2-3i)(6+4i) / (3+5i)
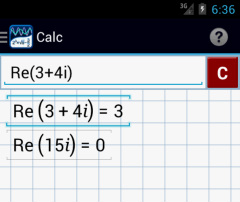
Real Number Part Function (Re)
Tap the i key twice to use the Re function. Given a complex number, this function will determine the real number part.
Examples
In each complex number below, identify the real number.
1. 3 + 4i
2. 15i
Calculator solutions
1) Tap i twice and type: 3 + 4i
2) Tap i twice and type: 15i
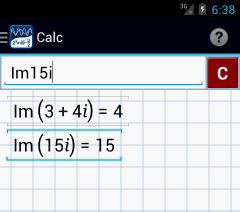
Imaginary Number Part Function (Im)
Tap the i key three times to use the Im function. Given a complex number, this function will identify the imaginary number part.
Examples
In each complex number below, identify the imaginary number.
1. 3 + 4i
2. 15i
Calculator solutions
1) Tap i three times and type: 3 + 4i
2) Tap i three times and type: 15i
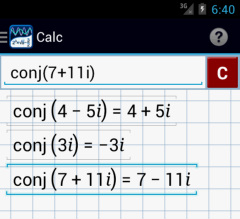
Complex Conjugate Function (conj)
Tap the i key four times to use the conj function. The conjugate of a complex number in the form a + bi is equal to a – bi. Use the conj function to determine the conjugate of a given complex number.
Examples
Write the conjugate of each complex number below.
1. 4 – 5i
2. 3i
3. 7 + 11i
Calculator solutions
1) Tap i four times and type: 4 – 5i
2) Tap i four times and type: 3i
3) Tap i four times and type: 7 + 11i
Complex Argument Function (arg)
Tap the i key five times to use the arg function. The argument of a complex number is the measurement of the angle (in standard position) that describes the direction of the complex number on the complex plane. It can be measured in radians or degrees.
Examples
Find the argument of each complex number below.
1. 4 – 5i
2. 3i
3. 7 + 11i
Calculator solutions
1) Tap i five times and type: 4 – 5i
2) Tap i five times and type: 3i
3) Tap i five times and type: 7 + 11i
Plotting The Imaginary Part of the Function
To plot the imaginary part of a function, type "Im" and enclose the expression of the given function.
Examples
Plot the imaginary part of each function below.
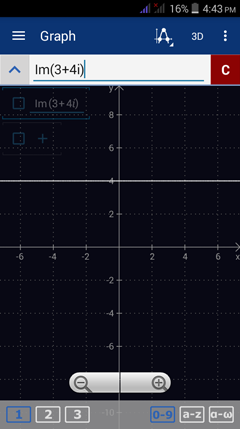
1) f(i) = 3 + 4i
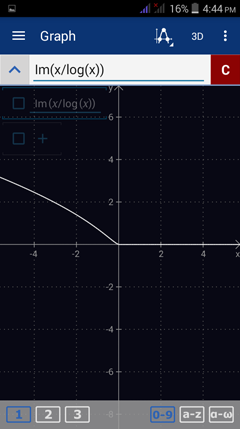
2) f(x) = x /log x
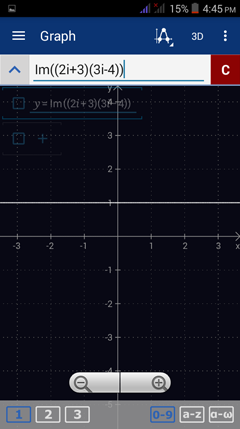
3) h(i) = (2i + 3)(3i - 4)
Calculator solutions
1) Type in: Im(3 + 4i)
Examples
Plot the imaginary part of each function below.
1) f(i) = 3 + 4i
2) f(x) = x /log x
3) h(i) = (2i + 3)(3i - 4)
Calculator solutions
1) Type in: Im(3 + 4i)
2) Type in: Im (x /log x)
3) Type in: Im((2i + 3)(3i - 4))