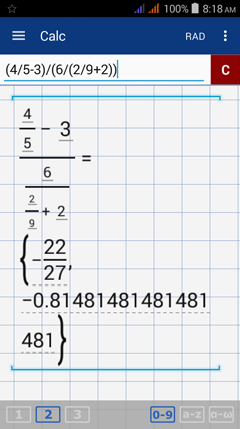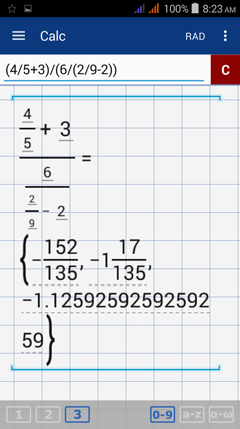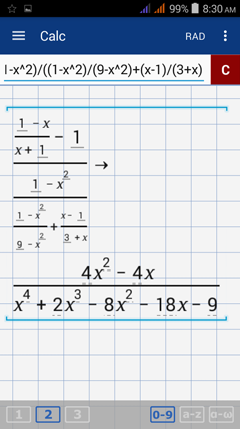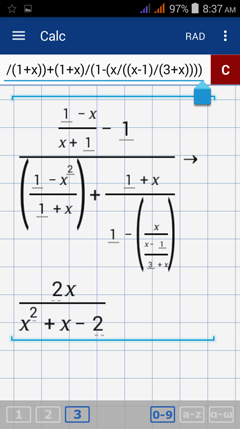6.2.2. Complex Fractions

Complex fractions have a fractional numerator, denominator, or both. Some examples are:

$\frac{\frac{4}{5}-3}{\frac{6}{\frac{2}{9}+2}}$

$\frac{\frac{3-1}{4}}{\frac{2+3}{\frac{2}{8}}}$

$\frac{\frac{3-x}{x+1}}{\frac{2+3x}{\frac{1-x^2}{9-x^2}+\frac{x-1}{3+x}}}$

$\frac{\frac{1-x}{x+1}-1}{\frac{1-x^2}{\frac{1-x^2}{9-x^2}+\frac{x-1}{3+x}}}$

$\frac{\frac{1-x}{x+1}-1}{{\frac{1-x^2}{1+x}+\frac{1+x}{1-\frac{x}{\frac{x-1}{3+x}}}}}$

$\frac{\frac{4}{5}}{\frac{6}{\frac{2}{9}+2}}$

To simplify complex fractions, begin by simplifying the numerator and denominator separately and rewrite the problem using the simplified fraction. Then multiply the fraction by the reciprocal of the denominator to bring the denominator up to the numerator.

Illustrative Example
Simplify the complex fraction:

$\frac{\frac{4}{5}-3}{\frac{6}{\frac{2}{9}+2}}$

Solution
Since both the numerator and denominator contain fractions, simplify them separately.

Step 1) Simplify the numerator by subtracting 3 from 4/5.
   4/5 - 3 = 4/5 - 15/5 = - 11/5

Step 2) Simplify the denominator of the denominator.
2/9 + 2 = 2/9 + 18/9 = 20/9

Step 3) Bring the denominator of the denominator up to the numerator.
  (-11/5) x (20/9) = (-220/45)

Step 4) Divide by the denominator 6.
  (-220/45) / 6 = (-220/ 270)

Step 5) Simplify.
  (-220/270) = -22/27 Final Answer

The app can perform all of these operations at once by grouping the fractions. An example is shown below.

Calculator Solution
Enter the expression as it appears in the problem: (4/5-3)/(6/(2/9+2))

Note: (4/5-3) is grouped in parentheses as the numerator. [6-(2/9+2)] is grouped as the denominator. Make sure that the grouping is correct and that there are no missing parentheses.

More Examples
Simplify each complex fraction

$1)\frac{\frac{3}{4}-1}{\frac{2}{3-\frac{2}{8+\frac{2}{3}}}}$

$2) \frac{\frac{4}{5}+3}{\frac{6}{\frac{2}{9}-2}}$

$3) \frac{\frac{3-x}{x+1}}{\frac{2+3x}{\frac{1-x^2}{9-x^2}+\frac{x-1}{3+x}}}$

$4) \frac{\frac{1-x}{x+1}-1}{\frac{1-x^2}{\frac{1-x^2}{9-x^2}+\frac{x-1}{3+x}}}$

$5) \frac{\frac{1-x}{x+1}-1}{{\frac{1-x^2}{1+x}+\frac{1+x}{1-\frac{x}{\frac{x-1}{3+x}}}}}$

Calculator Solutions

1) Enter the expression as it appears in the problem: ((3/4-1)/2)/(3-2/(8+2/3)

2) Enter the expression as it appears in the problem: (4/5+3)/(6/(2/9-2))

3) Enter the expression as it appears in the problem: ((3-x)/(x+2))/((2+3x)/((1-x^2)/(9-x^2)+( x-1)/(3+x))

4) Enter the expression as it appears in the problem: ((1-x)/(x+1)-1)/((1-x^2)/((1-x^2)/(9-x^2)+( x-1)/(3+x))

5) Enter the expression as it appears in the problem: ((1-x)/(x+1)-1)/(((1-x^2)/(1+x))+((1+x)/(1 -(x/((x-1)/(3+x))))

Next: Percents >

List of contents

﻿6.2.2. Complex Fractions﻿

6.2.2. Complex Fractions