1.3. Keyboard
Many of the keyboard buttons contain extra functions. These buttons include:
x ^, ln, i, x, sin, cos, tan, n!, degree key, /x/, root key, parentheses keys, and others.
To use these extra functions:
1) hold the button to see other functions available on that key
2) then
a) slide either left or right and select the function you want to enter, or
b) tap the button multiple times to switch between functions
The active function can be seen directly on the input field as you switch between the functions.
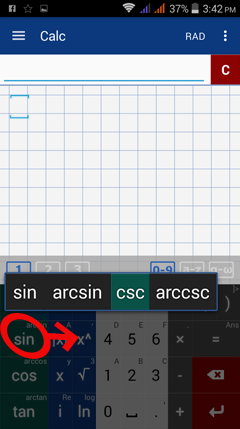
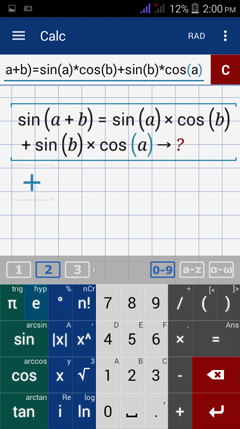
Below is a sample pop-up of the available functions under the sin (sine) key.
Other functions available on this key are arcsin (inverse of sine), csc (cosecant - the reciprocal of sine) and arccsc (arccosecant - the inverse of cosecant). The key highlighted in green is the active key.
x ^, ln, i, x, sin, cos, tan, n!, degree key, /x/, root key, parentheses keys, and others.
To use these extra functions:
1) hold the button to see other functions available on that key
2) then
a) slide either left or right and select the function you want to enter, or
b) tap the button multiple times to switch between functions
The active function can be seen directly on the input field as you switch between the functions.
Below is a sample pop-up of the available functions under the sin (sine) key.
Other functions available on this key are arcsin (inverse of sine), csc (cosecant - the reciprocal of sine) and arccsc (arccosecant - the inverse of cosecant). The key highlighted in green is the active key.
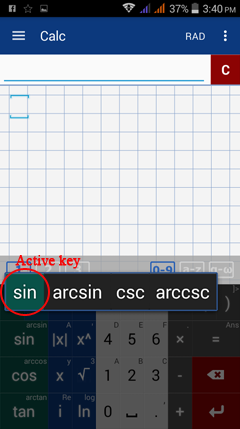
Hold sin and slide right to select csc, then release to enter. To cancel a selection, slide off of the pop-up and let go.
An alternative way to enter arcsin is to tap the sin key twice. Tap three times to enter csc. Tap four times to enter arccsc. Generally, the number of taps corresponds to the order of the function in the pop-ups. To use a certain key in the pop-up, just tap according to the order of the function you want to use.
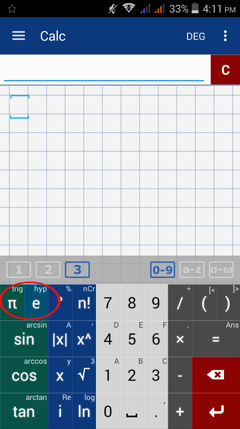
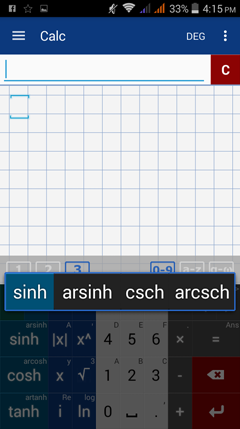
Hold e to switch to hyperbolic functions. Hold π to switch back to trigonometric functions.
Latin and Greek Keyboards
Use the keys on the top left of the main keyboard to switch between the default math keyboard, the Qwerty keyboard and the Greek keyboard.
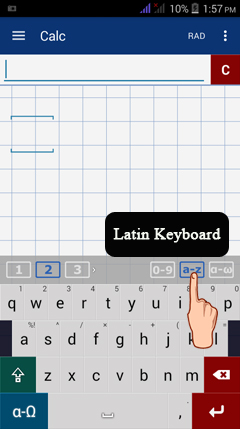
Latin Keyboard (a-z)
To enter an equation or argument using the Latin a-z characters, tap a-z to use the Qwerty keyboard.
Use the keys on the top left of the main keyboard to switch between the default math keyboard, the Qwerty keyboard and the Greek keyboard.
Latin Keyboard (a-z)
To enter an equation or argument using the Latin a-z characters, tap a-z to use the Qwerty keyboard.
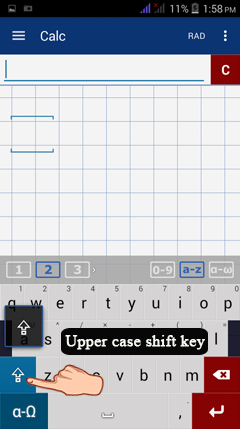
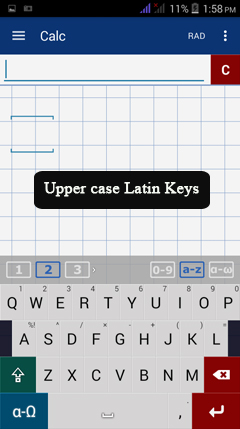
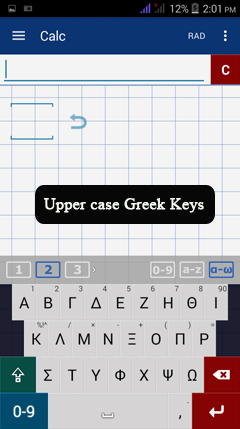
Tap the shift key to use uppercase letters.
See the example below.
Greek Keyboard
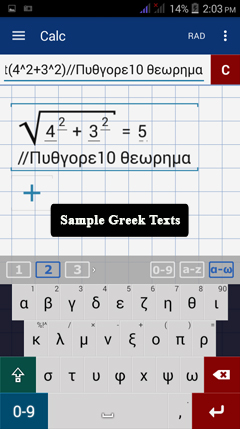
To enter an equation or arguments using Greek characters, switch to the Greek keyboard (α - ω).
To enter an equation or arguments using Greek characters, switch to the Greek keyboard (α - ω).
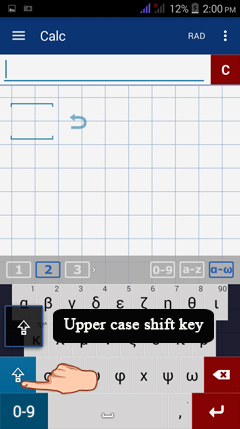
Tap the shift key to use uppercase Greek letters.
See the example below.
Resizing the Keyboard
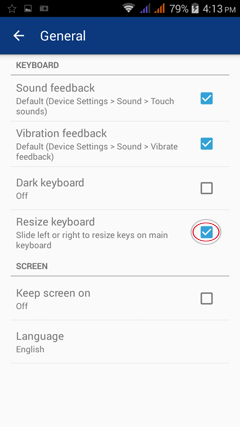
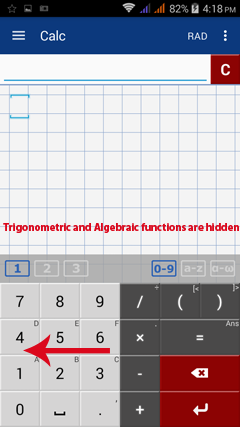
To hide keys not in use and/or enlarge other keys, resize your keyboard by dragging the default keyboard left or right.
You can enable this feature in: Settings > General > Resize keyboard. See the example in the following video:
To hide keys not in use and/or enlarge other keys, resize your keyboard by dragging the default keyboard left or right.
You can enable this feature in: Settings > General > Resize keyboard. See the example in the following video:
Keyboard map
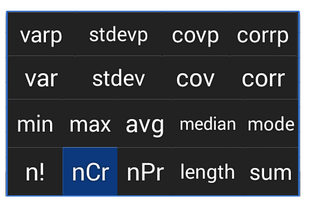
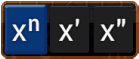
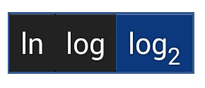
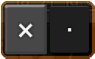
Below is a map of the keys and their respective pop-ups. The buttons shown in color are the main functions while the black buttons to the right are the extra functions listed under the same key.
The order of the function key in the pop-up list tells you how many times you need to tap to enter a function. For instance, the degree button also has the % and dms functions. The main function of this button is degree. To input the degree symbol, tap the button once. Tap twice for % and three times for dms.
Below is a map of the keys and their respective pop-ups. The buttons shown in color are the main functions while the black buttons to the right are the extra functions listed under the same key.
The order of the function key in the pop-up list tells you how many times you need to tap to enter a function. For instance, the degree button also has the % and dms functions. The main function of this button is degree. To input the degree symbol, tap the button once. Tap twice for % and three times for dms.
List of Pop-ups
|
Pop-up
|
Function
|
# of taps
|
|
sin
arcsin csc arccsc |
1
2 3 4 |
|
cos
arccos sec arcsec |
1
2 3 4 |
|
tan
arctan cot arccot |
1
2 3 4 |
|
cosh
arccosh sech arcsech |
1
2 3 4 |
|
sinh
arcsinh csch arcsch |
1
2 3 4 |
|
tanh
arctanh coth arccoth |
1
2 3 4 |
|
degree symbol
% dms |
1
2 3 |
|
n! (factorial key)
nCr nPr length sum min max avg median mode var stdev cov corr varp stdevp covp corrp |
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Note: Rather than counting the number of taps, it is easier to slide between the functions in the pop-up. |
|
/x/
//v// /A/ tr adj A^T, |
1
2 3 4 5 6 |
|
x ⁿ
x’ x” |
1
2 3 |
|
x
y z r θ t |
1
2 3 4 5 6 |
|
square root
cube root 4th root |
1
2 3 Note: to use the nth root, input a 4th root and replace the index "4" with the desired root. |
|
i
Re Im conj arg |
1
2 3 4 5 |
|
ln
log (base 10) log2 (log base 2) |
1
2 3 Note: to enter a logarithm with base n, tap 3 times for log2 and replace the index "2" with the desired base |
|
decimal point
comma |
1
2 |
|
fraction bar
division sign (same operation) |
1
2 |
|
multiplication sign
dot (same operation) |
1
2 |
|
open parentheses
open brackets less than symbol |
1
2 3 |
|
closed parentheses
closed brackets greater than symbol |
1
2 3 |
|
equal sign
Ans (lets you use the previous answer) |
1
2 |
|
Uppercase letters are often used to name a matrix, set, or when converting numbers from decimal to hexadecimal to binary to octal, or vice versa.
Hold 1 to enter A. Hold 2 to enter B. Hold 3 to enter C. Hold 4 to enter D. Hold 5 to enter E. Hold 6 to enter F. |
