15.8. Limit of a Trigonometric Function
The limits of trigonometric functions have the following properties:
Except for #7 and #8, the limit of a trigonometric function can be found by plugging in c. #7 and #8 are examples of indeterminate forms. For these properties, we can use the more appropriate method or L'Hôpital's rule for limits.
Illustrative Example
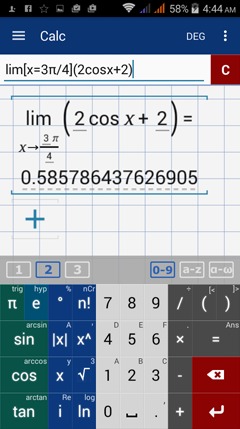
Calculate the limit of 2 cos x + 2 as x approaches 3π / 4.
Using the 2nd property, we can plug 3π / 4 into cosx as follows:
Using the 2nd property, we can plug 3π / 4 into cosx as follows:
= 0.585786437626905
Therefore
Therefore
Calculator Solution
Type in: lim [ x = 3π / 4 ] ( 2 cos x + 2 )
Type in: lim [ x = 3π / 4 ] ( 2 cos x + 2 )
More Examples
Calculate the limit of each trigonometric function if it exists.
Calculator solution
Type in: lim [ x = 0 ] ( x^2 cos( 1 / x ) )
Type in: lim [ x = 0 ] ( x^2 cos( 1 / x ) )
Calculator solution
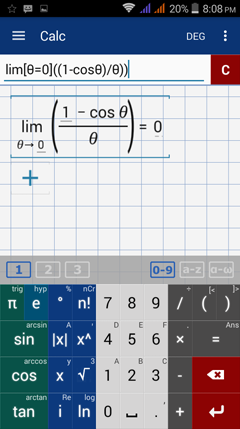
Type in: lim [ θ = 0 ] ( ( 1 - cosθ ) / θ )
Type in: lim [ θ = 0 ] ( ( 1 - cosθ ) / θ )
Calculator solution
Type in: lim [ x = 1 ] ( ( cos( x^2 -1 ) -1 ) / ( x^2 - 1 ) )
Type in: lim [ x = 1 ] ( ( cos( x^2 -1 ) -1 ) / ( x^2 - 1 ) )
Other Examples
Limit to Infinity
Some trigonometric functions such as tan, cot, sec and csc increase or decrease to positive or negative infinity respectively as x approaches c.
Illustrative Example
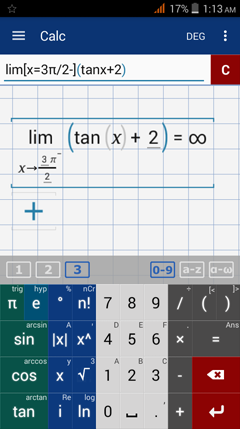
Calculate the limit of the given function below.
Illustrative Example
Calculate the limit of the given function below.
As x approaches 3π/2 from the left, the value of tan x increases to positive infinity such that the limit is ∞.
Calculator Solution
Type in: lim [ x = 3π/2 - ] ( tan x + 2 )
Calculator Solution
Type in: lim [ x = 3π/2 - ] ( tan x + 2 )
More Examples
Calculate each limit if it exists.
Calculate each limit if it exists.
Calculator Solution
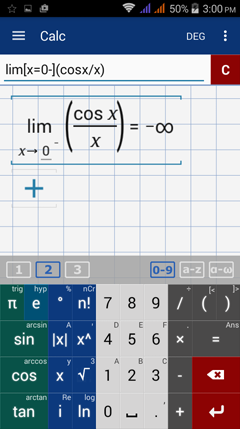
Type in: lim [ x = 0 - ] ( cos x / x )
Type in: lim [ x = 0 - ] ( cos x / x )
Calculator Solution
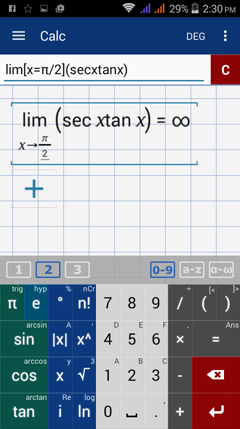
Type in: lim [ x = π/2 ] ( sec x tan x )
Type in: lim [ x = π/2 ] ( sec x tan x )
Limit Does Not Exist
Some trigonometric functions have asymptotes where the limit may not exist. See the examples below.
Examples
Calculate each limit if it exists.
Calculate each limit if it exists.
Calculator Solution
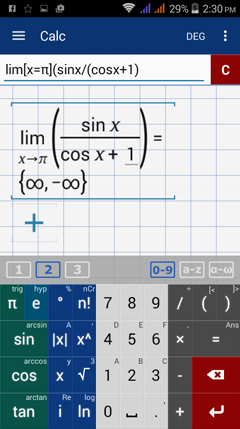
Type in: lim [ x = π ] ( sin x / ( cos x + 1 ) )
Type in: lim [ x = π ] ( sin x / ( cos x + 1 ) )
Calculator Solution
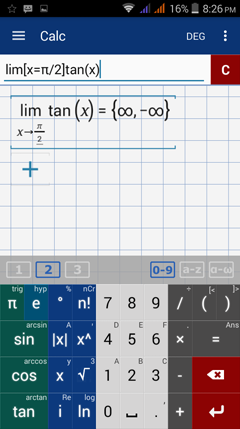
Type in: lim [ x = π/2 ] tan x
Type in: lim [ x = π/2 ] tan x
Calculator Solution
Type in: lim [ x = 0 ] cos x / x
Type in: lim [ x = 0 ] cos x / x