11.4. Linear Functions
A linear function is a function that can be written in the form f(x) = mx + b where m is the slope and b is the y-intercept. When graphing a linear function defined as f(x), only enter the function's expression, mx + b and set the domain if there are any restrictions.
Examples
Sketch the graph of the following linear function and note the direction of the line.
1) f(x) = 3x - 4
2) f(x) = 6(x - 2)
3) f(x) = 3(x + 1) - 5
4) f(x) = 2x - 3(x - 1)
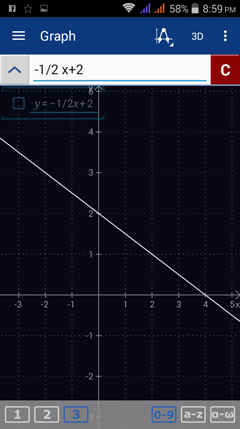
5) f(x) = - 1/2 x + 2
Calculator solutions
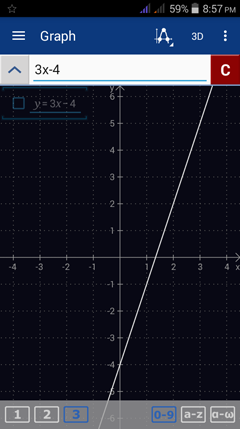
1) f(x) = 3x - 4
Enter the expression as it appears: 3x - 4
Examples
Sketch the graph of the following linear function and note the direction of the line.
1) f(x) = 3x - 4
2) f(x) = 6(x - 2)
3) f(x) = 3(x + 1) - 5
4) f(x) = 2x - 3(x - 1)
5) f(x) = - 1/2 x + 2
Calculator solutions
1) f(x) = 3x - 4
Enter the expression as it appears: 3x - 4
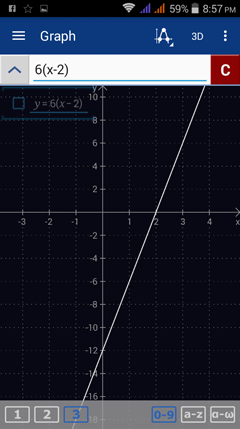
2) f(x) = 6(x - 2)
Enter the expression as it appears: 6(x - 2)
Enter the expression as it appears: 6(x - 2)
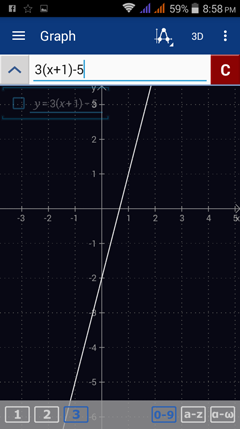
3) f(x) = 3(x + 1) - 5
Enter the expression as it appears: 3(x + 1) - 5
Enter the expression as it appears: 3(x + 1) - 5
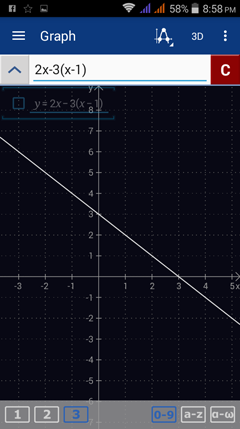
4) f(x) = 2x - 3(x - 1)
Enter the expression as it appears: 2x - 3(x - 1)
Enter the expression as it appears: 2x - 3(x - 1)
5) f(x) = - 1/2 x + 2
Enter the expression as it appears: - 1/2 x + 2
Enter the expression as it appears: - 1/2 x + 2